/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 30 kwietnia 2016 Czas pracy: 170 minut
Zadania zamknięte
Liczba 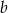 to 95% liczby
to 95% liczby  . Wskaż zdanie fałszywe.
. Wskaż zdanie fałszywe.
A) 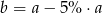 B)
B) 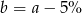 C)
C) 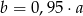 D)
D) 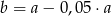
Wynikiem działania 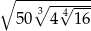 jest
jest
A) 10 B) 15 C) 100 D) 20
Liczbę 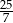 zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
A) 0,8% B) 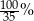 C) 8% D) 0,008%
C) 8% D) 0,008%
Liczba 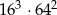 jest równa
jest równa
A) 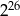 B)
B) 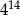 C)
C) 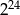 D)
D) 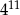
Liczba 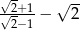 jest liczbą
jest liczbą
A) wymierną B) naturalną C) mniejszą niż 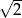 D) niewymierną
D) niewymierną
Liczba 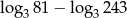 jest równa
jest równa
A) -1 B) 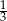 C) 3 D) -2
C) 3 D) -2
Wykres funkcji 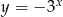 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) III i IV B) IV i I C) II i III D) I i II
Pole działki budowlanej jest równe 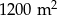 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 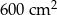 B)
B) 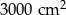 C)
C) 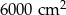 D)
D) 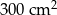
Rozwiązaniem równania 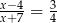 jest liczba
jest liczba
A) 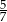 B) 37 C) 5 D)
B) 37 C) 5 D) 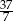
Na rysunku jest przedstawiony wykres funkcji 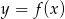 .
.
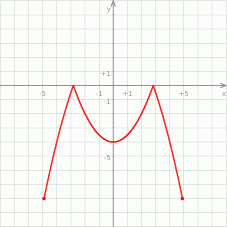
Które równanie ma dokładnie trzy rozwiązania?
A) 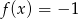 B)
B) 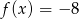 C)
C) 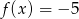 D)
D) 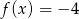
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
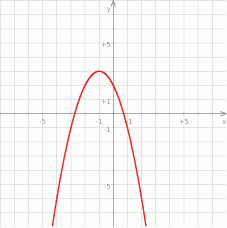
A) 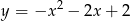 B)
B) 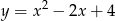 C)
C) 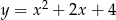 D)
D) 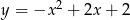
Wartość wyrażenia 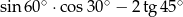 jest równa
jest równa
A) 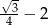 B)
B) 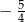 C)
C) 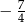 D)
D) 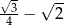
Do wykresu funkcji 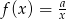 , dla
, dla 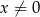 należy punkt
należy punkt 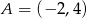 . Wtedy
. Wtedy
A) 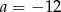 B)
B) 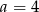 C)
C) 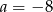 D)
D) 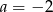
Liczby 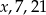 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 1 B) 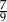 C)
C)  D)
D) 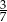
Na rysunku przedstawiony jest wykres funkcji liniowej 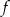 .
.
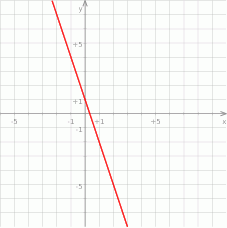
Funkcja 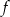 jest określona wzorem
jest określona wzorem
A) 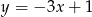 B)
B) 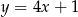 C)
C) 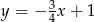 D)
D) 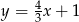
Wybieramy jedną liczbę ze zbioru 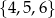 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 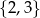 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 6 B) 3 C) 4 D) 5
W ciągu arytmetycznym piąty wyraz jest równy 11, a dziewiąty jest równy 25. Różnica tego ciągu jest równa
A) 7 B) 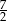 C)
C) 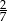 D) 14
D) 14
Działka budowlana ma wymiary podane na rysunku.
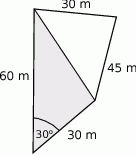
Powierzchnia zacieniowanego trójkąta jest równa
A) 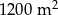 B)
B) 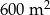 C)
C) 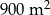 D)
D) 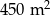
Punkty 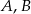 i
i 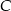 leżą na okręgu o środku
leżą na okręgu o środku 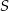 (zobacz rysunek).
(zobacz rysunek).
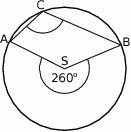
Miara zaznaczonego kąta wpisanego 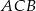 jest równa
jest równa
A) 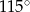 B)
B) 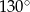 C)
C) 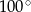 D)
D) 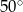
Które z równań opisuje prostą prostopadłą do prostej o równaniu 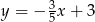 ?
?
A) 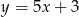 B)
B) 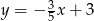 C)
C) 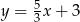 D)
D) 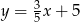
Ostrosłup ma 19 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 19 B) 36 C) 18 D) 38
Rysunek przedstawia wykres funkcji 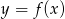 .
.
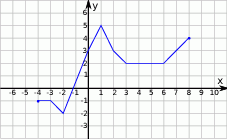
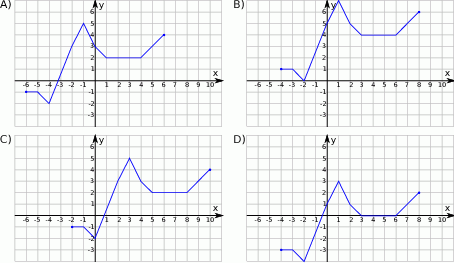
Wskaż wykres funkcji 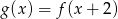 .
.
Powierzchnia sześcianu wynosi 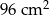 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 6 cm B) 5 cm C) 5,5 cm D) 4 cm
Dane są punkty 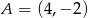 oraz
oraz 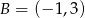 . Długość odcinka
. Długość odcinka 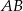 jest równa
jest równa
A) 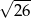 B)
B) 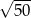 C)
C) 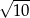 D)
D) 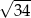
Prawdopodobieństwo zdarzenia 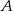 jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 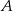 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 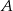 jest równe
jest równe
A) 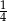 B)
B)  C)
C) 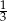 D)
D) 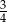
Zadania otwarte
Wykaż, że jeżeli 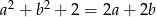 , to
, to 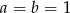 .
.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 2 cm krótsza od boku tego trójkąta.
Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 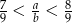 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 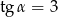 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 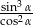 .
.
Dany jest trójkąt równoboczny 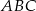 . Okrąg o średnicy
. Okrąg o średnicy 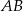 przecina bok
przecina bok 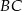 w punkcie
w punkcie 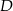 .
.
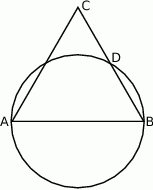
Wykaż, że 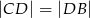 .
.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 6.
Kilku znajomych wybrało się na obiad, którego łączny koszt wyniósł 192 zł. Płacąc za obiad postanowili kwotę rachunku podzielić równo pomiędzy wszystkie obecne osoby. Okazało się jednak, że dwie osoby nie wzięły pieniędzy. W tej sytuacji każdy z pozostałych zapłacił o 8 zł więcej, niż powinien. Oblicz, ile osób uczestniczyło w obiedzie.
W trapezie równoramiennym 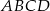 ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie 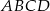 jest równy
jest równy 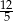 , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 12 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 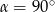 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.

