/Szkoła średnia/Zadania maturalne
Dowody w geometrii twierdzenie cosinusów poziom rozszerzony
Pole trójkąta 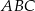 jest równe
jest równe 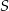 , a długości jego boków
, a długości jego boków 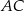 i
i 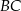 są odpowiednio równe
są odpowiednio równe 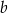 i
i  . Na bokach
. Na bokach 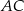 i
i 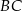 zbudowano kwadraty o środkach odpowiednio
zbudowano kwadraty o środkach odpowiednio 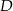 i
i 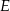 .
.
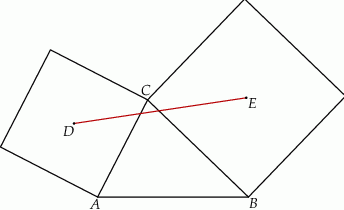
Wykaż, że
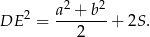
Wykaż, że istnieją dokładnie dwie liczby naturalne  takie, że trójkąt o bokach
takie, że trójkąt o bokach 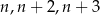 jest rozwartokątny.
jest rozwartokątny.
Wykaż, że jeżeli 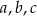 są długościami boków trójkąta to
są długościami boków trójkąta to 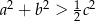 .
.
Kąt ostry równoległoboku ma miarę 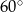 . Stosunek kwadratów długości przekątnych jest równy
. Stosunek kwadratów długości przekątnych jest równy 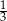 . Wykaż, że ten równoległobok jest rombem.
. Wykaż, że ten równoległobok jest rombem.
Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości wszystkich boków.
Kąt ostry rombu 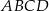 ma miarę
ma miarę 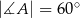 . Na bokach
. Na bokach 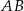 i
i 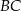 wybrano punkty
wybrano punkty 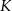 i
i 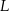 w ten sposób, że
w ten sposób, że 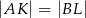 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 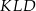 jest trójkątem równobocznym.
jest trójkątem równobocznym.
Wykaż, że jeżeli długości 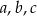 boków trójkąta spełniają równość
boków trójkąta spełniają równość
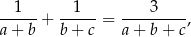
to promień okręgu opisanego na tym trójkącie jest równy 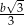 .
.
Przekątne trapezu 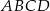 przecinają się w punkcie
przecinają się w punkcie 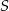 . Promień okręgu opisanego na trójkącie ostrokątnym
. Promień okręgu opisanego na trójkącie ostrokątnym 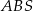 jest o 1 większy od promienia okręgu opisanego na trójkącie
jest o 1 większy od promienia okręgu opisanego na trójkącie 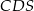 , a długości podstaw trapezu spełniają warunek
, a długości podstaw trapezu spełniają warunek 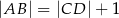 . Wykaż, że
. Wykaż, że
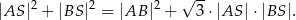
Dany jest trójkąt równoboczny 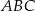 . Na bokach
. Na bokach 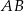 i
i 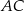 wybrano punkty – odpowiednio –
wybrano punkty – odpowiednio – 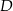 i
i 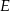 takie, że
takie, że 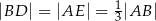 . Odcinki
. Odcinki 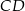 i
i 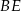 przecinają się w punkcie
przecinają się w punkcie 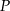 (zobacz rysunek).
(zobacz rysunek).
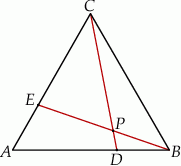
Wykaż, że pole trójkąta 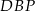 jest 21 razy mniejsze od pola trójkąta
jest 21 razy mniejsze od pola trójkąta 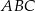 .
.
W trójkącie ostrokątnym 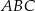 prawdziwa jest równość
prawdziwa jest równość 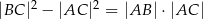 . Wykaż, że kąt
. Wykaż, że kąt 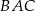 jest dwa razy większy od kąta
jest dwa razy większy od kąta 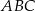 .
.
Czworokąt 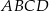 jest trapezem o podstawach
jest trapezem o podstawach 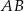 i
i 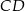 . Wykaż że
. Wykaż że
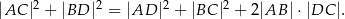
Czworokąt 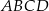 jest wpisany w okrąg oraz pola trójkątów
jest wpisany w okrąg oraz pola trójkątów 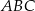 i
i 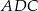 są równe. Wykaż, że
są równe. Wykaż, że
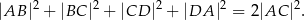
Dany jest czworokąt wypukły 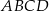 , w którym:
, w którym: 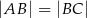 ,
, 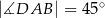 ,
, 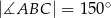 ,
, 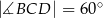 . Wykaż, że trójkąt
. Wykaż, że trójkąt 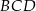 jest równoboczny.
jest równoboczny.

