/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 14 marca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 0,8 jest jednym z przybliżeń liczby 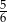 . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 0,025% B) 2,5% C) 4% D) 0,04%
Liczba 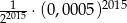 jest równa
jest równa
A) 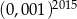 B)
B) 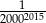 C)
C) 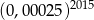 D)
D) 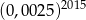
Punkty 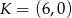 ,
, 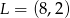 i
i 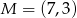 to środki boków, odpowiednio
to środki boków, odpowiednio 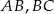 i
i 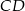 równoległoboku
równoległoboku 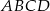 . Różnica długości przekątnych tego równoległoboku jest równa
. Różnica długości przekątnych tego równoległoboku jest równa
A) 4 B) 2 C) 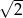 D)
D) 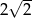
Liczba 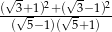 jest równa:
jest równa:
A) 4 B) 6 C) 2 D) 8
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 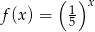 oraz
oraz 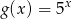 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 0 B) 1 C) 2 D) 3
Ile rozwiązań posiada równanie: 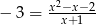 ?
?
A) 3 B) 2 C) 1 D) 0
Ciąg 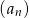 określony jest wzorem
określony jest wzorem 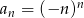 dla
dla 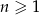 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 232 B) 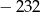 C) 96 D)
C) 96 D) 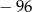
Prostą o równaniu 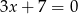 przekształcono w symetrii względem osi
przekształcono w symetrii względem osi 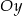 . W wyniku tego przekształcenia otrzymano prostą o równaniu
. W wyniku tego przekształcenia otrzymano prostą o równaniu
A) 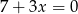 B)
B) 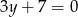 C)
C) 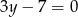 D)
D) 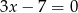
Liczba 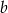 jest 2 razy większa od liczby
jest 2 razy większa od liczby  . Wtedy
. Wtedy
A) 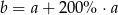 B)
B) 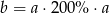 C)
C) 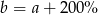 D)
D) 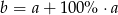
Liczba 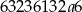 jest podzielna przez 4 jeżeli
jest podzielna przez 4 jeżeli
A) 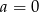 B)
B) 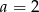 C)
C) 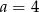 D)
D) 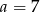
Funkcja 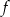 , określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie
, określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie  ostatnią cyfrę jej sześcianu. Zbiór wartości funkcji
ostatnią cyfrę jej sześcianu. Zbiór wartości funkcji 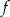 zawiera dokładnie
zawiera dokładnie
A) 5 elementów. B) 6 elementów. C) 9 elementów. D) 10 elementów.
Z sześcianu 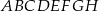 o krawędzi długości
o krawędzi długości  odcięto graniastosłup
odcięto graniastosłup 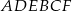 (zobacz rysunek).
(zobacz rysunek).
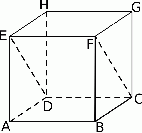
Ile razy objętość tego graniastosłupa jest mniejsza od objętości sześcianu?
A) 2 razy. B) 3 razy. C) 4 razy. D) 6 razy.
W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie 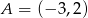 , która jest wykresem funkcji kwadratowej
, która jest wykresem funkcji kwadratowej 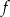 .
.
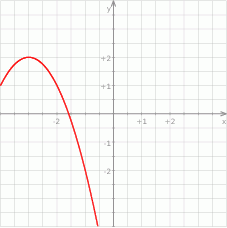
Funkcja 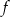 może być opisana wzorem
może być opisana wzorem
A) 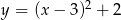 B)
B) 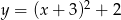 C)
C) 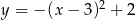 D)
D) 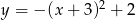
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 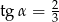 , to wartość wyrażenia
, to wartość wyrażenia 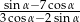 jest równa
jest równa
A) 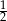 B)
B) 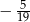 C)
C) 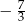 D)
D) 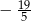
Liczby 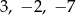 są trzema początkowymi wyrazami ciągu arytmetycznego
są trzema początkowymi wyrazami ciągu arytmetycznego 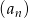 , określonego dla liczb naturalnych
, określonego dla liczb naturalnych 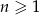 . Wzór ogólny tego ciągu ma postać
. Wzór ogólny tego ciągu ma postać
A) 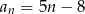 B)
B) 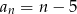 C)
C) 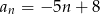 D)
D) 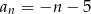
Wybierz równanie, które wraz z równaniem 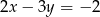 tworzy nieoznaczony układ równań.
tworzy nieoznaczony układ równań.
A) 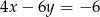 B)
B) 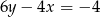 C)
C) 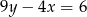 D)
D) 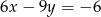
Dany jest trójkąt równoramienny, w którym ramię o długości 8 tworzy z podstawą kąt 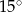 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 16 B) 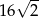 C)
C) 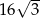 D) 32
D) 32
Funkcja liniowa 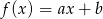 jest malejąca i ma dodatnie miejsce zerowe. Stąd wynika, że
jest malejąca i ma dodatnie miejsce zerowe. Stąd wynika, że
A) 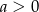 i
i 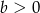 B)
B) 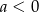 i
i 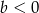 C)
C) 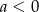 i
i 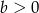 D)
D) 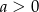 i
i 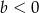
Kąt środkowy oparty na łuku, którego długość jest równa  długości okręgu, ma miarę
długości okręgu, ma miarę
A) 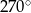 B)
B) 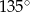 C)
C) 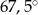 D)
D) 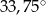
Rowerzysta połowę górskiej trasy pokonał ze średnią prędkością 8 km/h, a drugą połowę tej trasy pokonał ze średnią prędkością 24 km/h. Zatem średnia prędkość rowerzysty na całej trasie jest równa
A) 10 km/h B) 12 km/h C) 16 km/h D) 18 km/h
W jedenastowyrazowym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 4, a ostatni wyraz jest równy 36. Szósty wyraz tego ciągu jest równy
A) 12 B) 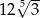 C)
C) 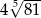 D) 20
D) 20
Kąt  jest ostry i
jest ostry i 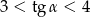 . Wtedy liczba
. Wtedy liczba 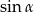 należy do przedziału
należy do przedziału
A) 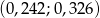 B)
B) 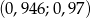 C)
C) 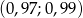 D)
D) 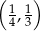
Stożek i walec mają takie same podstawy, a pole powierzchni bocznej walca jest dwa razy większe od pola powierzchni bocznej stożka. Wtedy tworząca stożka jest
A) dwa razy krótsza od wysokości walca.
B) trzy razy dłuższa od wysokości walca.
C) dwa razy dłuższa od wysokości walca.
D) równa wysokości walca.
Która z poniższych nierówności jest prawdziwa?
A) 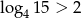 B)
B) 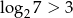 C)
C) 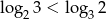 D)
D) 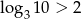
Rzucamy czterokrotnie symetryczną monetą. Prawdopodobieństwo, że otrzymamy co najmniej dwie reszki jest równe
A) 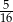 B)
B) 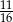 C)
C) 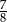 D)
D) 
Zadania otwarte
Rozwiąż nierówność 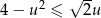 .
.
Rozwiąż równanie 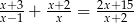 .
.
Wykaż, że dla dowolnej liczby całkowitej  liczba
liczba 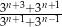 jest liczbą całkowitą.
jest liczbą całkowitą.
Gąsienica pełźnie po gałęzi do najbliższego smakowitego liścia, który jest odległy o 63,5 cm. Gąsienica jest jednak osłabiona i pełznie coraz wolniej. W pierwszej minucie udało jej się przebyć 32 cm, w drugiej pokonała drogę długości 16 cm, w trzeciej przepełznęła 8 cm itd. Po ilu minutach gąsienica dopełznie do liścia?
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to
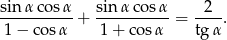
Objętość prostopadłościanu jest równa 405. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1 : 3 : 5. Oblicz pole powierzchni całkowitej prostopadłościanu.
Zakład rzemieślniczy otrzymał zlecenie wykonania partii detali. Do realizacji tego zamówienia wyznaczono trzy stanowiska tokarskie, przy czym wydajność stanowisk drugiego i trzeciego była odpowiednio o 20% i 40% mniejsza niż wydajność stanowiska pierwszego. Proces produkcji detali miał trwać 20 dni, ale po 13 dniach pierwsza tokarka uległa uszkodzeniu i proces produkcyjny dokończono przy pomocy dwóch pozostałych stanowisk. O ile dni wydłużyła się realizacja zamówienia?
Boki 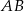 i
i 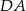 rombu
rombu 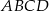 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 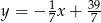 i
i 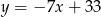 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 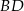 tego rombu, jeżeli jego środek ma współrzędne
tego rombu, jeżeli jego środek ma współrzędne 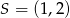 .
.
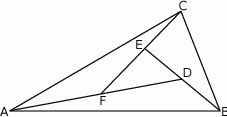
W trójkącie 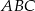 poprowadzono odcinki
poprowadzono odcinki 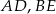 i
i 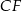 w ten sposób, że punkty
w ten sposób, że punkty 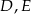 i
i 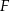 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 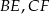 i
i 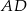 . Oblicz pole trójkąta
. Oblicz pole trójkąta 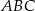 jeżeli pole trójkąta
jeżeli pole trójkąta 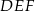 jest równe 2.
jest równe 2.