/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom podstawowy 29 września 2022 Czas pracy: 180 minut
Wartość wyrażenia 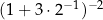 jest równa
jest równa
A) 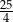 B)
B) 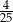 C)
C) 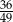 D)
D) 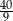
Wartość wyrażenia 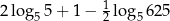 jest równa
jest równa
A) 1 B) 5 C) 10 D) 25
Wszystkich różnych liczb naturalnych czterocyfrowych, które są nieparzyste i podzielne przez 25, jest
A) 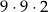 B)
B) 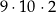 C)
C) 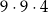 D)
D) 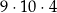
Dla każdej liczby rzeczywistej 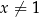 wyrażenie
wyrażenie 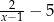 jest równe
jest równe
A) 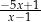 B)
B) 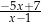 C)
C) 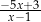 D)
D) 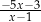
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 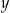 wyrażenie
wyrażenie
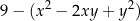
jest równe
A) ![[3− (x − 2y)]2](https://img.zadania.info/zes/0094475/HzesT19x.png) B)
B) ![[3+ (x− 2y)]2](https://img.zadania.info/zes/0094475/HzesT20x.png)
C) ![2 [3− (x+ 2y)]](https://img.zadania.info/zes/0094475/HzesT21x.png) D)
D) ![[3− (x− y)]⋅[3+ (x − y)]](https://img.zadania.info/zes/0094475/HzesT22x.png)
E) ![[3− (x + 2y)]⋅[3+ (x + 2y)]](https://img.zadania.info/zes/0094475/HzesT23x.png) F)
F) ![− [(x− y)− 3]⋅[(x − y) + 3]](https://img.zadania.info/zes/0094475/HzesT24x.png)
Rozwiąż równanie 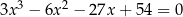 .
.
Równanie
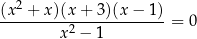
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 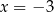
B) dwa rozwiązania: 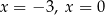
C) trzy rozwiązania: 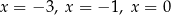
D) cztery rozwiązania: 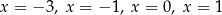
Wskaż nierówność, której zbiór wszystkich rozwiązań zaznaczono na osi liczbowej.
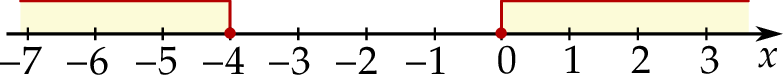
A) 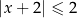 B)
B) 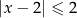 C)
C) 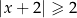 D)
D) 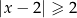
Klient banku wypłacił z bankomatu kwotę 1040 zł. Bankomat wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było dwa razy więcej niż 50–złotowych, a banknotów 20–złotowych było o 2 mniej niż 50–złotowych. Niech  oznacza liczbę banknotów 50–złotowych, a
oznacza liczbę banknotów 50–złotowych, a 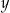 – liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb
– liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb  i
i 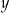 to
to
A) 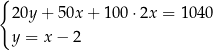 B)
B) 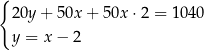
C) 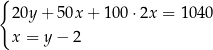 D)
D) 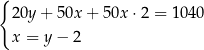
Informacja do zadań 10.1 – 10.3
Na rysunku, w kartezjańskim układzie współrzędnych 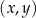 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 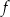 określonej dla każdego
określonej dla każdego 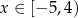 . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
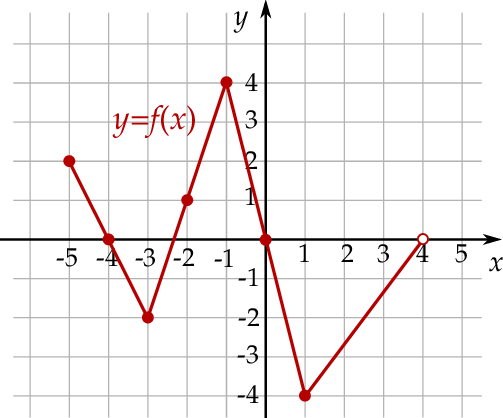
Wyznacz zbiór wartości funkcji 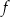 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dla każdego argumentu z przedziału 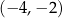 funkcja funkcja 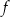 przyjmuje wartości ujemne. przyjmuje wartości ujemne. | P | F |
Funkcja 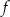 ma trzy miejsca zerowe. ma trzy miejsca zerowe. | P | F |
Najmniejsza wartość funkcji 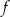 w przedziale
w przedziale ![[− 4,0]](https://img.zadania.info/zes/0094475/HzesT53x.png) jest równa
jest równa
A) 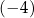 B)
B) 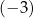 C)
C) 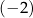 D) 0
D) 0
W kartezjańskim układzie współrzędnych 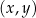 dane są: punkt
dane są: punkt 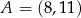 oraz okrąg o równaniu
oraz okrąg o równaniu 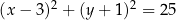 . Odległość punktu
. Odległość punktu 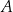 od środka tego okręgu jest równa
od środka tego okręgu jest równa
A) 25 B) 13 C) 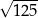 D)
D) 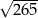
Informacja do zadań 12.1 i 12.2
Basen ma długość 25 m. W najpłytszym miejscu jego głębokość jest równa 1,2 m. Przekrój podłużny tego basenu przedstawiono poglądowo na rysunku. Głębokość 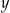 basenu zmienia się wraz z odległością
basenu zmienia się wraz z odległością  od brzegu w sposób opisany funkcją:
od brzegu w sposób opisany funkcją:
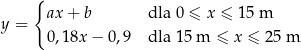
Odległość  jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości
jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości  i
i 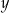 są wyrażone w metrach.
są wyrażone w metrach.
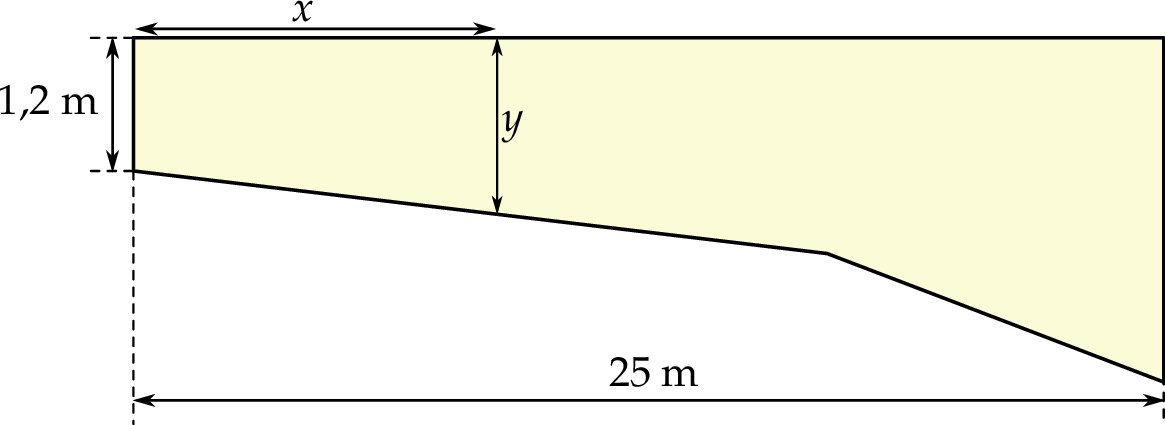
Największa głębokość basenu jest równa
A) 5,4 m B) 3,6 m C) 2,2 m D) 1,8 m
Oblicz wartość współczynnika  oraz wartość współczynnika
oraz wartość współczynnika 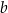 .
.
Informacja do zadań 13.1 i 13.2
Funkcja kwadratowa 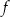 jest określona wzorem
jest określona wzorem 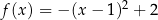 .
.
Wykresem funkcji 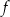 jest parabola, której wierzchołek ma współrzędne
jest parabola, której wierzchołek ma współrzędne
A) 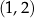 B)
B) 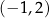 C)
C) 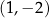 D)
D) 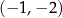
Zbiorem wartości funkcji 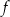 jest przedział
jest przedział
A) ![(− ∞ ,2]](https://img.zadania.info/zes/0094475/HzesT80x.png) B)
B) 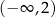 C)
C) 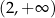 D)
D) 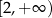
Informacja do zadań 14.1 i 14.2
Dany jest ciąg 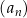 określony wzorem
określony wzorem 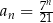 dla każdej liczby naturalnej
dla każdej liczby naturalnej 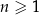 .
.
Pięćdziesiątym wyrazem ciągu 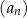 jest
jest
A) 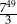 B)
B) 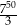 C)
C) 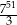 D)
D) 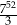
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ciąg 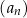 jest geometryczny. jest geometryczny. | P | F |
Suma trzech początkowych wyrazów ciągu 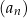 jest równa 20. jest równa 20. | P | F |
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 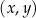 , dana jest prosta
, dana jest prosta 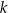 o równaniu
o równaniu 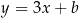 , przechodząca przez punkt
, przechodząca przez punkt 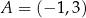 . Współczynnik
. Współczynnik 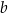 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 6 C) 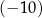 D) 8
D) 8
Informacja do zadań 16.1 – 16.3
Dany jest ciąg 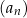 określony wzorem
określony wzorem 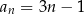 dla każdej liczby naturalnej
dla każdej liczby naturalnej 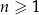 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A, B albo C oraz jej uzasadnienie 1, 2 albo 3.
Ciąg 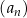 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 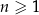
1) 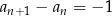 , , | 2) 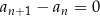 , , | 3) 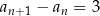 , , |
Najmniejszą wartością  , dla której wyraz
, dla której wyraz 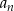 jest większy od 25, jest
jest większy od 25, jest
A) 8 B) 9 C) 7 D) 26
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 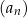 jest równa 57 dla
jest równa 57 dla  równego
równego
A) 6 B) 23 C) 5 D) 11
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 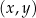 , dane są:
, dane są:
– prosta 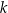 o równaniu
o równaniu 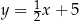
– prosta 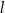 o równaniu
o równaniu 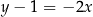 .
.
Proste 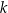 i
i 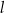
A) pokrywają się. B) nie mają punktów wspólnych.
C) są prostopadłe. D) przecinają się pod kątem 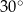 .
.
Wartość wyrażenia 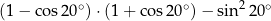 jest równa
jest równa
A) 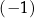 B) 0 C) 1 D) 20
B) 0 C) 1 D) 20
W pojemniku są wyłącznie kule białe i czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 4 : 5. Z pojemnika losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
A)  B)
B)  C)
C)  D)
D) 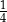
Punkty 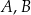 oraz
oraz 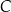 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 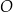 . Kąt
. Kąt 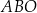 ma miarę
ma miarę 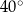 , a kąt
, a kąt 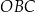 ma miarę
ma miarę 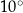 (zobacz rysunek).
(zobacz rysunek).
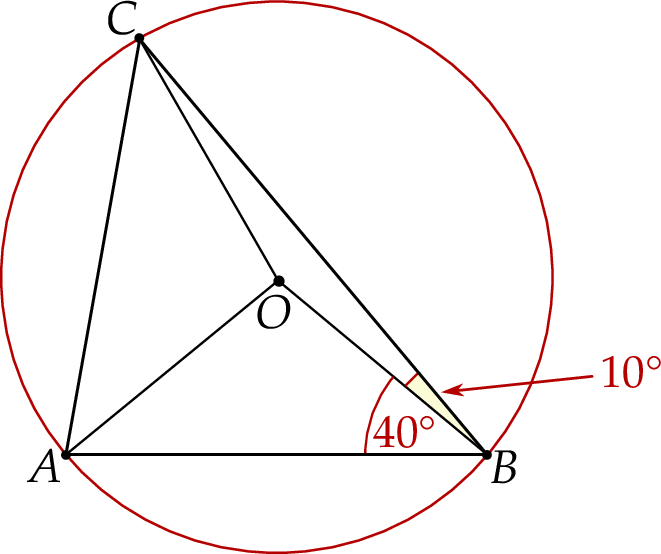
Miara kąta 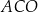 jest równa
jest równa
A) 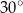 B)
B) 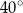 C)
C) 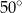 D)
D) 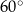
Dany jest trójkąt 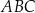 o bokach długości 6, 7 oraz 8. Oblicz cosinus największego kąta tego trójkąta.
o bokach długości 6, 7 oraz 8. Oblicz cosinus największego kąta tego trójkąta.
W trójkącie 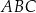 bok
bok 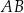 ma długość 4, a bok
ma długość 4, a bok 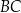 ma długość 4,6. Dwusieczna kąta
ma długość 4,6. Dwusieczna kąta 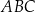 przecina bok
przecina bok 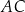 w punkcie
w punkcie 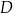 takim, że
takim, że 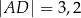 (zobacz rysunek).
(zobacz rysunek).
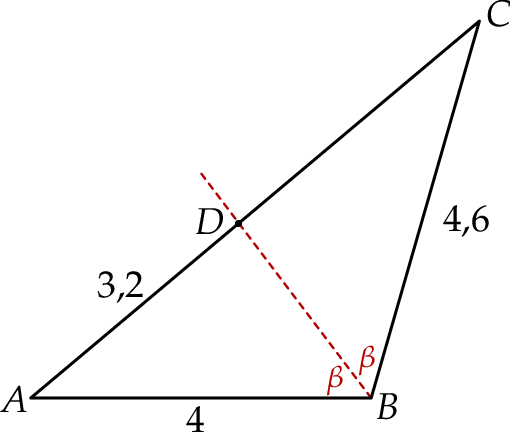
Odcinek 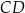 ma długość
ma długość
A) 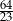 B)
B) 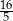 C)
C) 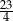 D)
D) 
Rodzinna firma stolarska produkuje małe wiatraki ogrodowe. Na podstawie analizy rzeczywistych wpływów i wydatków stwierdzono, że przychód 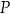 (w złotych) z tygodniowej sprzedaży
(w złotych) z tygodniowej sprzedaży  wiatraków można opisać funkcją
wiatraków można opisać funkcją
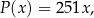
a koszt 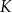 (w złotych) produkcji
(w złotych) produkcji  wiatraków w ciągu jednego tygodnia można określić funkcją
wiatraków w ciągu jednego tygodnia można określić funkcją
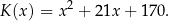
Tygodniowo w zakładzie można wyprodukować co najwyżej 150 wiatraków. Oblicz, ile tygodniowo wiatraków należy sprzedać, aby zysk zakładu w ciągu jednego tygodnia był największy. Oblicz ten największy zysk.
Informacja do zadań 24.1 – 24.3
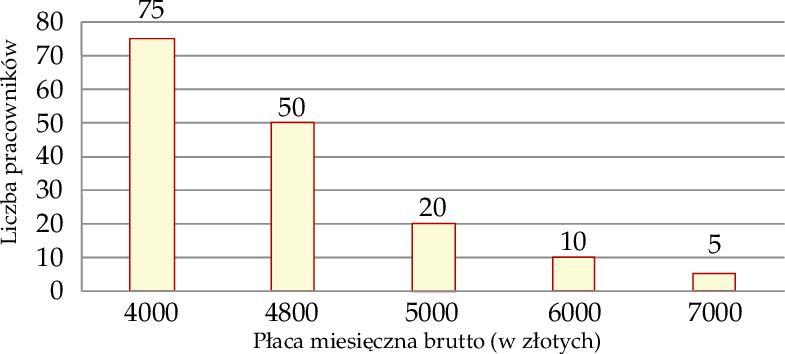
Firma  zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy  , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
Średnia miesięczna płaca brutto w firmie  jest równa
jest równa
A) 4 593,75 zł B) 4 800,00 zł C) 5 360,00 zł D) 2 399,33 zł
Mediana miesięcznej płacy pracowników firmy  jest równa
jest równa
A) 4 000 zł B) 4 800 zł C) 5 000 zł D) 5 500 zł
Liczba pracowników firmy  , których miesięczna płaca brutto nie przewyższa 5 000 zł, stanowi (w zaokrągleniu do 1%)
, których miesięczna płaca brutto nie przewyższa 5 000 zł, stanowi (w zaokrągleniu do 1%)
A) 91% liczby wszystkich pracowników tej firmy.
B) 78% liczby wszystkich pracowników tej firmy.
C) 53% liczby wszystkich pracowników tej firmy.
D) 22% liczby wszystkich pracowników tej firmy.
Każda z krawędzi podstawy trójkątnej ostrosłupa ma długość 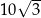 , a każda jego krawędź boczna ma długość 15. Oblicz wysokość tego ostrosłupa.
, a każda jego krawędź boczna ma długość 15. Oblicz wysokość tego ostrosłupa.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 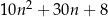 przy dzieleniu przez 5 daje resztę 3.
przy dzieleniu przez 5 daje resztę 3.

