/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 14 kwietnia 2018 Czas pracy: 170 minut
Zadania zamknięte
Liczba 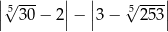 jest równa
jest równa
A) 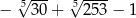 B)
B) 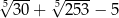 C)
C) 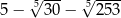 D)
D) 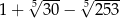
Dane są dwa sześciany. Pole powierzchni całkowitej pierwszego sześcianu jest większe od pola powierzchni całkowitej drugiego sześcianu o 30%. Wynika stąd, że objętość pierwszego sześcianu jest większa od objętości drugiego sześcianu
A) o mniej niż 50%, ale więcej niż 40%. B) o mniej niż 60% , ale więcej niż 50%.
C) o mniej niż 70% , ale więcej niż 60%. D) o więcej niż 70%.
Liczba 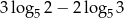 jest równa
jest równa
A) 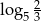 B)
B) 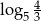 C)
C) 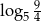 D)
D) 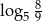
Na rysunku przedstawiono fragment wykresu funkcji 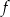 określonej wzorem
określonej wzorem 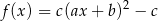 .
.
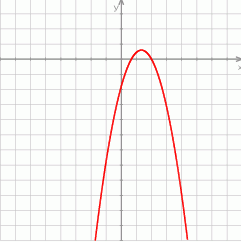
Współczynniki 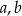 i
i  spełniają warunki:
spełniają warunki:
A) 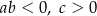 B)
B) 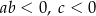 C)
C) 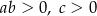 D)
D) 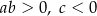
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 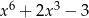 jest równe
jest równe
A) 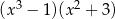 B)
B) 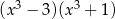 C)
C) 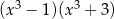 D)
D) 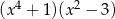
Kąt  jest rozwarty i
jest rozwarty i 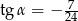 . Wobec tego
. Wobec tego
A) 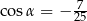 B)
B) 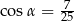 C)
C) 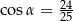 D)
D) 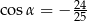
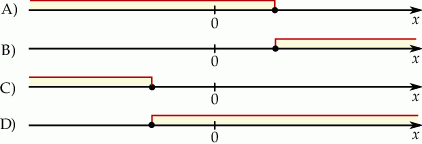
Wskaż rysunek, na którym może być przedstawiony zbiór wszystkich rozwiązań nierówności 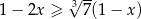 .
.
Rozwiązaniem układu równań 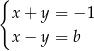 z niewiadomymi
z niewiadomymi  i
i 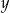 jest para liczb ujemnych. Wynika stąd, że
jest para liczb ujemnych. Wynika stąd, że
A) 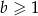 B)
B) 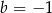 C)
C) 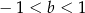 D)
D) 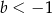
Liczba 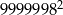 jest równa
jest równa
A) 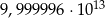 B)
B) 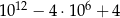 C)
C) 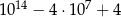 D)
D) 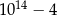
Równanie 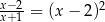
A) ma dokładnie trzy rozwiązania. B) ma dokładnie dwa rozwiązania.
C) ma dokładnie jedno rozwiązanie. D) nie ma rozwiązań.
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 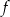 określonej wzorem
określonej wzorem 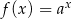 . Punkt
. Punkt 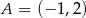 należy do tego wykresu funkcji.
należy do tego wykresu funkcji.
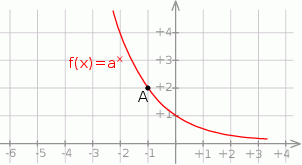
Podstawa  potęgi jest równa
potęgi jest równa
A) 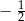 B)
B) 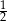 C)
C) 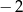 D) 2
D) 2
Punkt 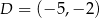 jest obrazem punktu
jest obrazem punktu 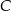 w symetrii względem punktu
w symetrii względem punktu 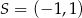 , a punkt
, a punkt 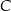 jest środkiem odcinka
jest środkiem odcinka 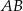 , gdzie
, gdzie 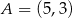 . Punkt
. Punkt 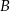 ma współrzędne
ma współrzędne
A) 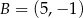 B)
B) 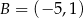 C)
C) 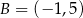 D)
D) 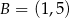
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 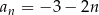 , gdzie
, gdzie 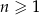 jest równa
jest równa 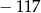 . Zatem
. Zatem
A) 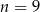 B)
B) 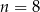 C)
C) 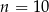 D)
D) 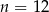
Trapez równoramienny 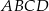 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 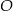 (zobacz rysunek).
(zobacz rysunek).
Różnica miar kątów 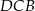 i
i 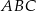 tego trapezu jest równa
tego trapezu jest równa
A) 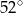 B)
B) 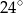 C)
C) 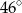 D)
D) 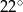
Dany jest ciąg geometryczny 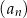 , określony dla
, określony dla 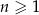 , o którym wiemy, że:
, o którym wiemy, że: 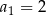 i
i 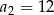 . Wtedy
. Wtedy 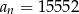 dla
dla
A) 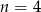 B)
B) 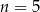 C)
C) 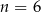 D)
D) 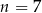
Odchylenie standardowe zestawu danych: 2, 3, 4, 5, 6 jest równe
A) 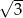 B) 2 C)
B) 2 C) 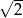 D) 4
D) 4
W trójkącie 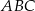 punkt
punkt 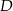 leży na boku
leży na boku 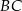 , a punkt
, a punkt 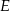 leży na boku
leży na boku 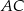 . Odcinek
. Odcinek 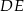 jest równoległy do boku
jest równoległy do boku 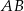 , a ponadto
, a ponadto 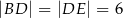 ,
, 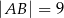 (zobacz rysunek).
(zobacz rysunek).
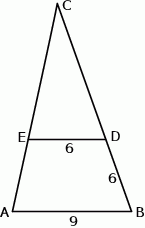
Odcinek 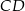 ma długość
ma długość
A) 8 B) 4 C) 9 D) 12
Dany jest trójkąt równoboczny, którego pole jest równe 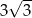 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 3 B) 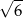 C) 6 D)
C) 6 D) 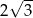
Samochód pokonał trasę długości 115 km w ciągu 46 minut. Gdyby samochód jadąc z tą samą prędkością średnią miał pokonać odległość 240 km, to zajęłoby to
A) 94 minuty. B) 90 minut. C) 96 minut. D) 88 minut.
Punkty 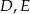 i
i 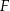 są środkami krawędzi
są środkami krawędzi 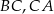 i
i 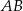 podstawy
podstawy 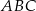 ostrosłupa trójkątnego
ostrosłupa trójkątnego 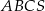 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 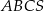 do objętości ostrosłupa
do objętości ostrosłupa 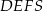 jest równy
jest równy
A) 4 B) 8 C) 3 D) 9
Prosta 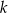 przechodzi przez punkt
przechodzi przez punkt 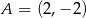 i jest prostopadła do osi
i jest prostopadła do osi 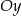 . Prosta
. Prosta 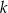 ma równanie
ma równanie
A) 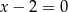 B)
B) 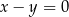 C)
C) 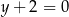 D)
D) 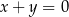
Graniastosłup ma 16 wierzchołków. Liczba wszystkich krawędzi tego graniastosłupa jest równa
A) 16 B) 32 C) 20 D) 24
Obwód podstawy stożka wynosi 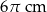 . Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
. Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
A) 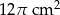 B)
B) 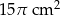 C)
C) 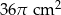 D)
D) 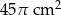
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania pary liczb, których iloczyn jest większy od 18, jest równe
A) 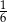 B)
B) 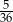 C)
C)  D)
D) 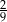
Zadania otwarte
Wykaż, że liczba 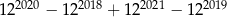 jest podzielna przez 429.
jest podzielna przez 429.
Rozwiąż nierówność 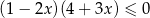 .
.
Środkowa 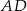 trójkąta
trójkąta 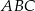 ma długość równą połowie długości boku
ma długość równą połowie długości boku 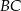 oraz
oraz 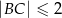 . Wykaż, że
. Wykaż, że 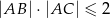 .
.
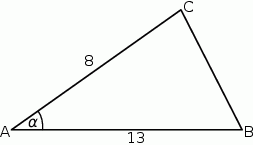
W trójkącie 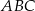 dane są długości boków
dane są długości boków 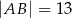 i
i 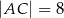 oraz
oraz 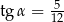 , gdzie
, gdzie 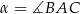 . Oblicz pole trójkąta
. Oblicz pole trójkąta 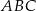 .
.
Iloczyn pierwszego i piątego wyrazu malejącego ciągu arytmetycznego 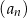 jest równy 160, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę jeden. Wyznacz różnicę tego ciągu.
jest równy 160, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę jeden. Wyznacz różnicę tego ciągu.
Ze zbioru liczb 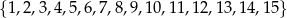 losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę
losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 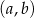 , gdzie
, gdzie  jest wynikiem pierwszego losowania,
jest wynikiem pierwszego losowania, 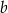 jest wynikiem drugiego losowania. Oblicz, ile jest wszystkich par
jest wynikiem drugiego losowania. Oblicz, ile jest wszystkich par 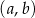 takich, że iloczyn
takich, że iloczyn 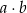 jest liczbą podzielną przez 3.
jest liczbą podzielną przez 3.
Funkcja kwadratowa 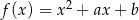 ma dwa miejsca zerowe, które różnią się o 7. Wykres funkcji
ma dwa miejsca zerowe, które różnią się o 7. Wykres funkcji 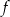 przechodzi przez punkt
przechodzi przez punkt 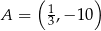 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 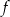 .
.
Dane są punkty 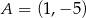 i
i 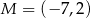 oraz prosta
oraz prosta 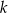 o równaniu
o równaniu 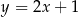 . Wierzchołek
. Wierzchołek 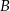 trójkąta
trójkąta 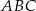 to punkt przecięcia prostej
to punkt przecięcia prostej 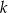 z prostą
z prostą 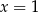 , a wierzchołek
, a wierzchołek 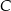 jest punktem przecięcia prostej
jest punktem przecięcia prostej 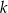 z prostą
z prostą 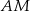 . Oblicz pole trójkąta
. Oblicz pole trójkąta 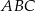 .
.
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa 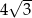 i tworzy z krawędzią boczną kąt
i tworzy z krawędzią boczną kąt  taki, że
taki, że 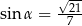 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

