/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom rozszerzony 19 grudnia 2022 Czas pracy: 180 minut

Zadanie 1

(2 pkt)

Oblicz

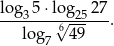
log3-5⋅lo√g-2527. log7 6 49

Informacja do zadań 2.1 i 2.2

Funkcja 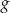jest określona wzorem 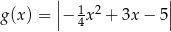| | g(x) = ||− 1x 2 + 3x − 5|| 4 dla każdego 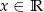x ∈ R . Fragment wykresu funkcji 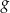w kartezjańskim układzie współrzędnych 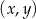(x ,y) przedstawiono na rysunku (jednostki pominięto).

Zadanie 2.1

(2 pkt)

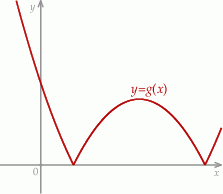
Wyznacz zbiór wszystkich wartości, jakie funkcja 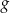przyjmuje w przedziale [9,11] .

Zadanie 2.2

(2 pkt)

Wyznacz zbiór wszystkich wartości parametru 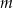, dla których równanie 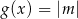g(x ) = |m | ma dokładnie dwa rozwiązania dodatnie.

Zadanie 3

(3 pkt)

Wykaż, że dla każdej liczby rzeczywistej oraz dla każdej liczby rzeczywistej 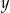, spełniających warunek 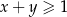x + y ≥ 1 , prawdziwa jest nierówność

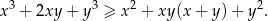
3 3 2 2 x + 2xy + y ≥ x + xy (x+ y)+ y .

Zadanie 4

(3 pkt)

Maszyna napełnia torebki herbatą. Każda torebka ma zostać napełniona 200 g herbaty. Torebkę, która zawiera mniej niż 200 g herbaty, nazywamy torebką z niedowagą. Prawdopodobieństwo tego, że pojedyncza torebka napełniona przez tę maszynę jest z niedowagą, jest równe 0,1. Kontroli poddano masę herbaty w torebkach napełnianych przez tę maszynę danego dnia. Do kontroli wybrano losowo 20 torebek. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród tych 20 losowo wybranych torebek znajdą się co najwyżej dwie torebki z niedowagą.

Zadanie 5

(4 pkt)

Rozwiąż równanie

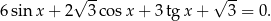
√ -- √ -- 6 sin x + 2 3 cos x+ 3tg x+ 3 = 0.

Zadanie 6

(4 pkt)

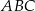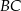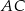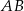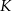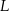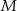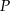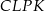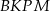W trójkącie ABC poprowadzono dwusieczne kątów przecinające boki , i tego trójkąta w punktach – odpowiednio – , oraz . Punkt jest punktem przecięcia tych dwusiecznych. Na czworokątach CLP K oraz BKP M można opisać okrąg. Udowodnij, że trójkąt 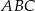ABC jest równoboczny.

Zadanie 7

(4 pkt)

Olejarnia wytwarza olej ekologiczny. Aby produkcja była opłacalna, dzienna wielkość produkcji musi wynosić co najmniej 480 litrów i nie może przekroczyć 530 litrów (ze względu na ograniczone moce produkcyjne). Przy poziomie produkcji 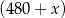(48 0+ x) litrów dziennie przeciętny koszt 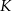(w złotych) wytworzenia jednego litra oleju jest równy

2 K(x ) = 22x--−-62-1,5x-+-23430-, gdzie x ∈ [0,50] 480+ x

Oblicz, ile litrów oleju dziennie powinna wytworzyć olejarnia, aby przeciętny koszt produkcji jednego litra oleju był najmniejszy (z zachowaniem opłacalności produkcji). Oblicz ten najmniejszy przeciętny koszt.

Zadanie 8

(5 pkt)

Rozwiąż nierówność

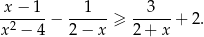
x-−--1-− --1---≥ --3---+ 2 . x2 − 4 2 − x 2 + x

Zadanie 9

(5 pkt)

Wyznacz wszystkie wartości parametru 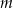, dla których równanie

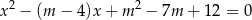
2 2 x − (m − 4)x + m − 7m + 12 = 0

ma dwa różne rozwiązania rzeczywiste 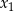x 1 oraz 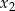, spełniające warunek

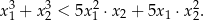
x31 + x32 < 5x 21 ⋅x 2 + 5x 1 ⋅x22.

Zadanie 10

(5 pkt)

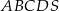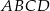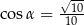Dany jest ostrosłup prawidłowy czworokątny ABCDS o podstawie ABCD . Krawędź podstawy tego ostrosłupa ma długość . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze takim, że √-10- cosα = 10 . Przez krawędź 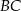podstawy ostrosłupa poprowadzono płaszczyznę 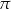prostopadłą do ściany bocznej 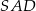SAD . Sporządź rysunek tego ostrosłupa, zaznacz na rysunku przekrój wyznaczony przez płaszczyznę 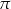i nazwij ﬁgurę, która jest tym przekrojem. Oblicz pole otrzymanego przekroju.

Zadanie 11

(5 pkt)

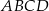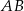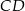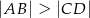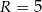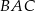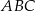Dany jest trapez ABCD o podstawach i , w którym |AB | > |CD | oraz ramię ma długość 6. Na tym trapezie opisano okrąg o promieniu R = 5 . Miary kątów BAC i ABC tego trapezu spełniają warunek

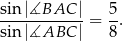
sin-|∡BAC--|- 5- sin |∡ABC | = 8.

Oblicz pole i obwód trapezu 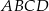ABCD .

Zadanie 12

(6 pkt)

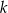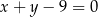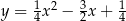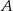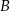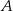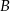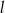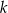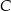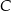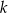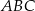Prosta o równaniu x + y − 9 = 0 przecina parabolę o równaniu y = 14x2 − 32x + 14 w punktach oraz . Pierwsza współrzędna punktu jest liczbą dodatnią; pierwsza współrzędna punktu jest liczbą ujemną. Prosta jest równoległa do prostej i styczna do danej paraboli w punkcie . Oblicz odległość punktu od prostej oraz pole trójkąta ABC .