/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 30 marca 2019 Czas pracy: 170 minut
Zadania zamknięte
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 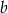 stanowi 96% liczby
stanowi 96% liczby 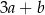 oraz 120% liczby
oraz 120% liczby 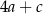 . Wynika stąd, że
. Wynika stąd, że
A) 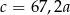 B)
B) 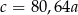 C)
C) 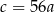 D)
D) 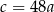
Wskaż liczbę spełniającą nierówność 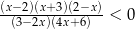 .
.
A) 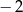 B)
B) 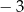 C) 5 D)
C) 5 D) 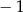
Dane są liczby 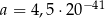 oraz
oraz 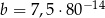 . Wtedy iloraz
. Wtedy iloraz 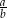 jest równy
jest równy
A) 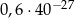 B)
B) 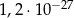 C)
C) 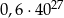 D)
D) 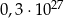
Dane są liczby 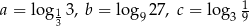 . Liczby te spełniają warunek
. Liczby te spełniają warunek
A) 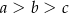 B)
B) 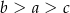 C)
C) 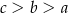 D)
D) 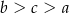
Liczba 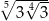 jest równa
jest równa
A) 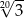 B)
B) 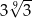 C)
C) 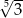 D)
D) 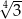
Wyrażenie 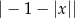 dla
dla 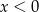 jest równe
jest równe
A) 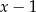 B)
B) 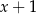 C)
C) 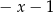 D)
D) 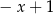
Równanie 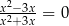
A) ma trzy rozwiązania: 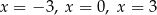
B) ma jedno rozwiązanie: 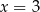
C) ma dwa rozwiązania: 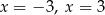
D) ma dwa rozwiązania: 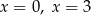
Na rysunku jest przedstawiona graficzna ilustracja układu trzech równań stopnia pierwszego z dwiema niewiadomymi  i
i 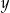 .
.
Wskaż ten układ
A) 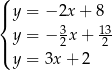 B)
B) 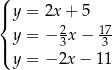 C)
C) 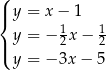 D)
D) 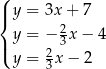
Liczba 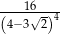 jest równa
jest równa
A) 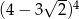 B)
B) 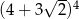 C)
C) 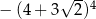 D)
D) 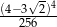
Funkcja 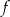 jest określona wzorem
jest określona wzorem 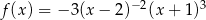 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 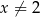 . Wartość funkcji
. Wartość funkcji 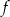 dla argumentu
dla argumentu 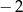 jest równa
jest równa
A) 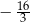 B)
B) 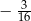 C)
C) 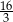 D)
D) 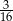
Punkt 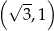 należy do wykresu funkcji
należy do wykresu funkcji 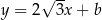 . Wtedy współczynnik
. Wtedy współczynnik 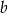 jest równy
jest równy
A) 7 B) 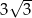 C)
C) 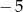 D)
D) 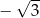
Ciąg 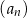 określony jest wzorem
określony jest wzorem 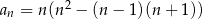 , gdzie
, gdzie 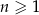 . Suma piętnastu początkowych wyrazów tego ciągu jest równa
. Suma piętnastu początkowych wyrazów tego ciągu jest równa
A) 240 B) 105 C) 120 D) 136
Wykres funkcji 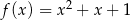 przesunięto o 2 jednostki w prawo i 1 jednostkę w górę. W wyniku tej operacji otrzymano wykres funkcji
przesunięto o 2 jednostki w prawo i 1 jednostkę w górę. W wyniku tej operacji otrzymano wykres funkcji
A) 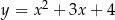 B)
B) 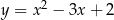
C) 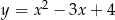 D)
D) 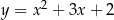
Wszystkie wyrazy ciągu geometrycznego 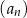 określonego dla
określonego dla 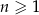 są dodatnie i
są dodatnie i 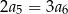 . Stąd wynika, że iloraz
. Stąd wynika, że iloraz 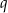 tego ciągu jest równy
tego ciągu jest równy
A) 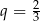 B)
B) 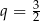 C)
C) 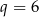 D)
D) 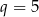
Dany jest trójkąt o bokach długości 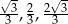 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 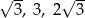 B)
B) 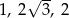 C)
C) 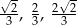 D)
D) 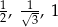
Pole koła przedstawionego na rysunku jest równe
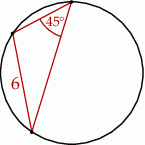
A) 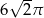 B)
B) 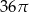 C)
C) 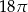 D)
D) 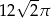
Liczba 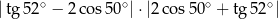 jest równa
jest równa
A) 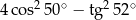 B)
B) 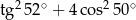
C) 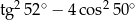 D)
D) 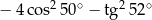
Różnica miar dwóch kątów rozwartych trapezu jest równa 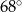 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 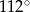 B)
B) 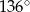 C)
C) 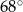 D)
D) 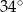
Prosta 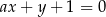 jest równoległa do prostej
jest równoległa do prostej 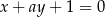 . Wtedy
. Wtedy
A) 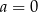 B)
B) 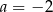 C)
C) 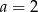 D)
D) 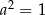
Dany jest walec, w którym promień podstawy, wysokość i średnica podstawy są kolejnymi wyrazami ciągu geometrycznego. Pole powierzchni całkowitej tego walca jest równe 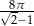 . Wynika stąd, że promień podstawy tego walca jest równy
. Wynika stąd, że promień podstawy tego walca jest równy
A) 9 B) 6 C) 3 D) 2
Punkt 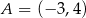 jest końcem odcinka
jest końcem odcinka 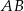 , a punkt
, a punkt 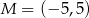 jest takim punktem tego odcinka, że
jest takim punktem tego odcinka, że 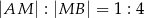 . Długość odcinka
. Długość odcinka 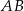 jest równa
jest równa
A) 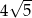 B)
B) 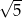 C)
C) 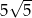 D)
D) 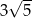
Przekątna prostokątna ma długość 6, a długość jego krótszego boku jest równa 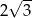 . Kąt rozwarty
. Kąt rozwarty  między przekątnymi tego prostokąta spełnia warunek
między przekątnymi tego prostokąta spełnia warunek
A) 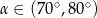 B)
B) 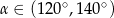 C)
C) 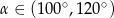 D)
D) 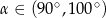
Wysokość graniastosłupa prawidłowego trójkątnego jest równa połowie długości jego krawędzi podstawy. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
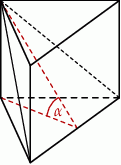
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 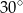 B)
B) 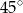 C)
C) 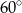 D)
D) 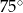
W zestawie 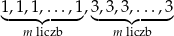 jest
jest 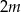 liczb (
liczb (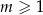 ), w tym
), w tym 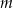 liczb 1 i
liczb 1 i 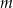 liczb 3. Odchylenie standardowe tego zestawu liczb jest równe
liczb 3. Odchylenie standardowe tego zestawu liczb jest równe
A) 1 B) 2 C) 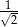 D)
D) 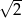
W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwa razy w czterech losowaniach wyciągniemy kulę koloru czarnego, jest równe
A) 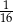 B)
B) 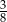 C)
C) 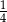 D)
D) 
Zadania otwarte
Rozwiąż nierówność 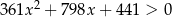 .
.
Rozwiąż równanie 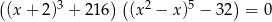 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 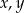 prawdziwa jest nierówność
prawdziwa jest nierówność 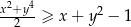 .
.
Na bokach 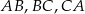 trójkąta równobocznego
trójkąta równobocznego 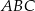 wybrano kolejno punkty
wybrano kolejno punkty 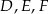 tak, że
tak, że 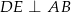 ,
, 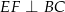 i
i 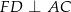 .
.
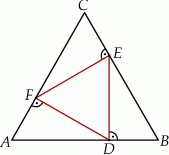
Wykaż, że trójkąt 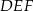 jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta 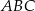 .
.
Udowodnij, że jeżeli liczby 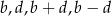 są różne od zera oraz
są różne od zera oraz 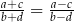 , to
, to 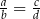 .
.
Dwudziesty wyraz ciągu arytmetycznego 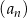 , określonego dla
, określonego dla 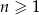 , jest równy 395, a suma jego dwudziestu początkowych wyrazów jest równa 8930. Oblicz pierwszy wyraz tego ciągu.
, jest równy 395, a suma jego dwudziestu początkowych wyrazów jest równa 8930. Oblicz pierwszy wyraz tego ciągu.
Trasa rowerowa wokół jeziora ma długość 12 kilometrów. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro w tym samym kierunku. Średnia prędkość jednego z nich jest o 4 km/h mniejsza niż prędkość drugiego rowerzysty. Do ponownego spotkania rowerzystów doszło, gdy szybszy z nich wykonał 4 okrążenia jeziora. Jakie były średnie prędkości rowerzystów?
Punkty 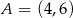 i
i 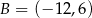 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 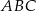 , w którym
, w którym 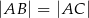 . Wysokość
. Wysokość 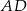 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 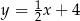 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 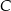 tego trójkąta.
tego trójkąta.
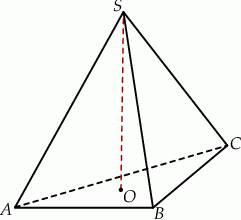
W ostrosłupie prawidłowym trójkątnym 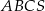 cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy
cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy 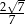 . Wykaż, że pole powierzchni bocznej tego ostrosłupa stanowi
. Wykaż, że pole powierzchni bocznej tego ostrosłupa stanowi  jego pola powierzchni całkowitej.
jego pola powierzchni całkowitej.