/Szkoła średnia/Zadania maturalne

Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom rozszerzony 31 maja 2011 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

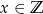Niech x ∈ Z . Wykaż, że wyrażenie 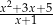x2+-3x+5- x+1 przyjmuje wartość całkowitą tylko dla czterech wartości x . Podaj te liczby.

Zadanie 2
(5 pkt)

Wyznaczyć sinusy kątów ostrych trójkąta prostokątnego wiedząc, że stosunek promieni okręgów opisanego i wpisanego w ten trójkąt jest równy 5 2 .

Zadanie 3
(6 pkt)

Dla jakich wartości parametru 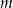m jeden pierwiastek równania 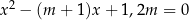x2 − (m + 1 )x+ 1,2m = 0 jest równy sinusowi, a drugi cosinusowi tego samego kąta ostrego?

Zadanie 4
(4 pkt)

Wykaż, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność:

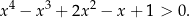
x4 − x3 + 2x2 − x + 1 > 0 .

Zadanie 5
(4 pkt)

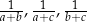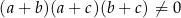Liczby -1-- -1---1-- a+b ,a+c,b+c , gdzie (a + b)(a + c)(b + c) ⁄= 0 są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że liczby 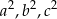a2,b2,c2 są również wyrazami ciągu arytmetycznego.

Zadanie 6
(4 pkt)

Pole prostokąta jest równe 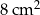8 cm 2 . Wyznacz jeden z boków prostokąta, jako funkcję drugiego boku i naszkicuj wykres tej funkcji. Podaj dziedzinę i zbiór wartości tej funkcji.

Zadanie 7
(5 pkt)

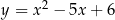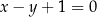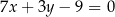Napisz równanie okręgu, do którego należą punkty wspólne paraboli y = x2 − 5x + 6 i prostej x− y+ 1 = 0 , a którego środek należy do prostej o równaniu 7x + 3y − 9 = 0 .

Zadanie 8
(4 pkt)

Naszkicuj wykres funkcji 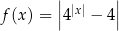|| || f (x) = |4|x| − 4| . Na podstawie wykresu określ przedziały, w których funkcja jest rosnącą.

Zadanie 9
(4 pkt)

Promień koła wpisanego w trapez prostokątny jest równy r , kąt ostry trapezu równy jest α . Oblicz pole i obwód trapezu.

Zadanie 10
(5 pkt)

W trójkąt prostokątny o przyprostokątnych długości 6 i 8 wpisujemy prostokąt w taki sposób, że dwa jego boki zawarte są w przyprostokątnych, a jeden z jego wierzchołków leży na przeciwprostokątnej. Zbadaj, jakie powinny być wymiary prostokąta, aby jego pole było możliwie największe.

Zadanie 11
(5 pkt)

Trzynasty wyraz ciągu geometrycznego jest równy 10. Oblicz wartość iloczynu dwudziestu pięciu początkowych wyrazów tego ciągu.

Arkusz Wersja PDF
Rozwiązania