/Szkoła średnia/Zadania maturalne
Poprawkowy Egzamin Maturalny
z Matematyki poziom podstawowy 23 sierpnia 2016 Czas pracy: 170 minut
Zadania zamknięte
Suma pięciu kolejnych liczb całkowitych jest równa 195. Najmniejszą z tych liczb jest
A) 37 B) 38 C) 39 D) 40
Buty, które kosztowały 220 złotych, przeceniono i sprzedano za 176 złotych. O ile procent obniżono cenę butów?
A) 80 B) 20 C) 22 D) 44
Liczba 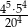 jest równa
jest równa
A) 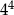 B)
B) 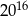 C)
C) 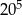 D) 4
D) 4
Liczba 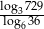 jest równa
jest równa
A) 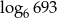 B) 3 C)
B) 3 C) 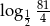 D) 4
D) 4
Najmniejszą liczbą całkowitą spełniającą nierówność 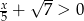 jest
jest
A) 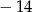 B)
B) 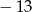 C) 13 D) 14
C) 13 D) 14
Funkcja kwadratowa określona jest wzorem 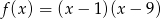 . Wynika stąd, że funkcja
. Wynika stąd, że funkcja 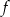 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 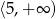 B)
B) 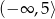 C)
C) 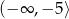 D)
D) 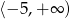
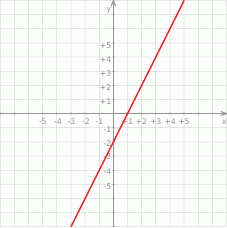
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 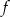 , przy czym
, przy czym 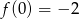 i
i 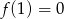 .
.
Wykres funkcji 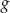 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 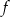 względem początku układu współrzędnych. Funkcja
względem początku układu współrzędnych. Funkcja 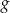 jest określona wzorem
jest określona wzorem
A) 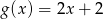 B)
B) 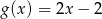 C)
C) 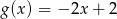 D)
D) 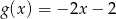
Pierwszy wyraz ciągu geometrycznego jest równy 8, a czwarty wyraz tego ciągu jest równy 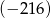 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 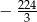 B)
B) 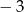 C)
C) 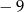 D)
D) 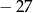
Kąt  jest ostry i
jest ostry i 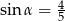 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 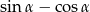 jest równa
jest równa
A) 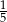 B)
B) 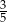 C)
C) 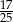 D)
D) 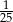
Jeśli funkcja kwadratowa 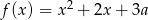 nie ma ani jednego miejsca zerowego, to liczba
nie ma ani jednego miejsca zerowego, to liczba  spełnia warunek
spełnia warunek
A) 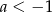 B)
B) 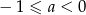 C)
C) 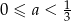 D)
D) 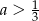
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 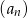 jest określona wzorem
jest określona wzorem 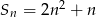 . Wtedy wyraz
. Wtedy wyraz 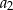 jest równy
jest równy
A) 3 B) 6 C) 7 D) 10
Układ równań 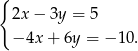
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma nieskończenie wiele rozwiązań
Liczba 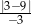 jest równa
jest równa
A) 2 B) 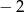 C) 0 D)
C) 0 D) 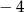
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 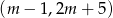 , gdzie
, gdzie 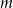 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 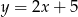 B)
B) 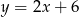 C)
C) 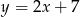 D)
D) 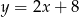
Kąt rozwarcia stożka ma miarę 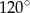 , a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
A) 3 B) 6 C) 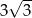 D)
D) 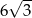
Wartość wyrażenia 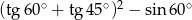 jest równa
jest równa
A) 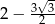 B)
B) 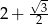 C)
C) 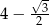 D)
D) 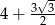
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
A) 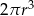 B)
B) 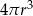 C)
C) 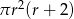 D)
D) 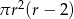
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 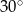 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 32 B) 16 C) 12 D) 8
Punkty 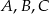 i
i  leżą na okręgu o środku
leżą na okręgu o środku 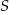 . Cięciwa
. Cięciwa 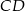 przecina średnicę
przecina średnicę 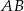 tego okręgu w punkcie
tego okręgu w punkcie 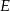 tak, że
tak, że 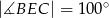 . Kąt środkowy
. Kąt środkowy 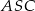 ma miarę
ma miarę 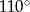 (zobacz rysunek).
(zobacz rysunek).
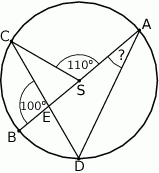
Kąt wpisany 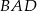 ma miarę
ma miarę
A) 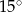 B)
B) 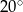 C)
C) 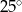 D)
D) 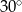
Okręgi o środkach 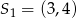 oraz
oraz 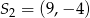 i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
A) 8 B) 6 C) 5 D) 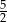
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 2, a przekątna ściany bocznej ma długość 3 (zobacz rysunek). Kąt, jaki tworzą przekątne ścian bocznych tego graniastosłupa wychodzące z jednego wierzchołka, ma miarę  .
.
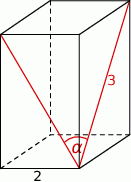
Wtedy wartość 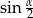 jest równa
jest równa
A)  B)
B) 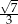 C)
C) 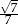 D)
D) 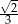
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa 11. Podstawą tego ostrosłupa jest
A) dziesięciokąt. B) jedenastokąt. C) dwunastokąt. D) trzynastokąt.
Jeżeli do zestawu czterech danych: 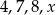 dołączymy liczbę 2, to średnia arytmetyczna wzrośnie o 2. Zatem
dołączymy liczbę 2, to średnia arytmetyczna wzrośnie o 2. Zatem
A) 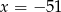 B)
B) 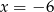 C)
C) 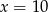 D)
D) 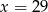
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 3?
A) 12 B) 24 C) 29 D) 30
Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że wynikiem rzutu są dwa orły i sześć oczek na kostce, jest równe
A) 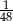 B)
B) 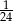 C)
C) 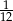 D)
D) 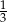
Zadania otwarte
Rozwiąż nierówność 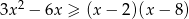 .
.
Jeżeli do licznika pewnego nieskracalnego ułamka dodamy 32, a mianownik pozostawimy niezmieniony, to otrzymamy liczbę 2. Jeżeli natomiast od licznika i od mianownika tego ułamka odejmiemy 6, to otrzymamy liczbę 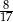 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Wykaż, że jeżeli liczby rzeczywiste 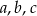 spełniają warunek
spełniają warunek 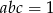 , to
, to
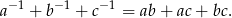
Funkcja kwadratowa jest określona wzorem 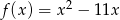 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 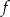 w przedziale
w przedziale 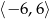 .
.
W trapezie 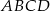 o podstawach
o podstawach 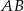 i
i 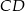 przekątne
przekątne 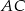 oraz
oraz 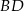 przecinają się w punkcie
przecinają się w punkcie 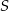 . Wykaż, że jeżeli
. Wykaż, że jeżeli 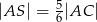 , to pole trójkąta
, to pole trójkąta 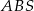 jest 25 razy większe od pola trójkąta
jest 25 razy większe od pola trójkąta 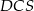 .
.
Ciąg arytmetyczny 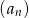 określony jest wzorem
określony jest wzorem 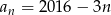 , dla
, dla 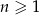 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego 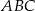 :
: 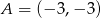 i
i 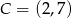 oraz prosta o równaniu
oraz prosta o równaniu 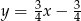 , zawierająca przeciwprostokątną
, zawierająca przeciwprostokątną 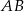 tego trójkąta.
tego trójkąta.
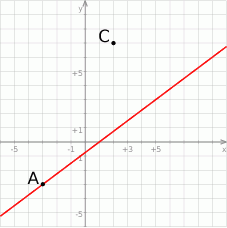
Oblicz współrzędne wierzchołka 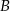 tego trójkąta i długość odcinka
tego trójkąta i długość odcinka 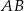 .
.
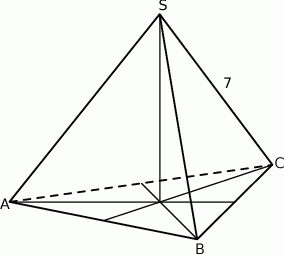
Trójkąt równoboczny 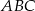 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 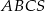 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 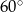 , a krawędź boczna ma długość 7 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
, a krawędź boczna ma długość 7 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
Ze zbioru siedmiu liczb naturalnych 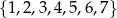 losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.
losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.

