/Szkoła średnia/Zadania maturalne
Prawdopodobieństwo warunkowe XII Polygon Matematyczny poziom rozszerzony Styczeń 2020
Zdarzenia losowe 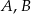 są zawarte w
są zawarte w 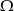 oraz
oraz 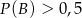 . Wykaż, że
. Wykaż, że
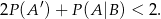
O zdarzeniach losowych 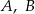 wiadomo, że:
wiadomo, że: 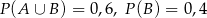 i
i 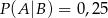 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 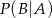 .
.
Znając prawdopodobieństwa zdarzeń 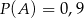 ,
, 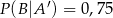 ,
, 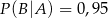 , gdzie
, gdzie 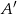 oznacza zdarzenie przeciwne do
oznacza zdarzenie przeciwne do 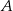 , oblicz prawdopodobieństwo zdarzenia
, oblicz prawdopodobieństwo zdarzenia 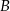 .
.
Rzucamy dwukrotnie kostką do gry. Jakie jest prawdopodobieństwo, że suma wyrzuconych oczek jest większa niż 9, jeżeli wiadomo, że dokładnie jeden raz wypadło 6 oczek?
Sześciokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników są dokładnie trzy dwójki. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy piątkę?
Z talii 52 kart w czterech kolorach wybieramy losowo 2 karty. Oblicz prawdopodobieństwo, że wybrane karty to król i as, przy założeniu, że wybrane karty mają różne kolory.
Doświadczenie losowe polega na tym, że losujemy jednocześnie trzy liczby ze zbioru
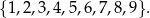
Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb będzie liczba 3, pod warunkiem, że suma wylosowanych liczb będzie nieparzysta. Wynik przedstaw w postaci ułamka nieskracalnego.
Z pojemnika zawierającego 10 kul białych i 6 czarnych losujemy jedną kulę i wkładamy zamiast niej jedną kulę czarną. Oblicz prawdopodobieństwo tego, że jeżeli teraz wylosujemy z pojemnika dwie kule, to obie wylosowane kule będą białe.
Rzucamy raz sześcienną kostką do gry, a następnie rzucamy tyloma monetami, ile oczek wypadło na kostce. Oblicz prawdopodobieństwo tego, że dokładnie na jednej z wyrzuconych monet jest reszka. Wynik podaj w postaci ułamka nieskracalnego.
Rzucamy trzy razy monetą, a następnie rzucamy tyle razy kostką, ile orłów otrzymaliśmy w rzutach monetami. Oblicz prawdopodobieństwo tego, że suma oczek otrzymanych w rzutach kostką jest dwa razy większa od liczby orłów otrzymanych w rzutach monetą jeżeli wiadomo, że w rzutach monetą otrzymaliśmy przynajmniej jednego orła.
Z talii 52 kart wylosowano dwie karty i, nie oglądając ich, włożono do drugiej talii. W ten sposób powstała talia złożona z 54 kart. Oblicz prawdopodobieństwo wylosowania asa z tak utworzonej talii kart.
Zestaw tematów egzaminacyjnych składa się z 15 tematów z algebry, 15 z geometrii i  tematów z prawdopodobieństwa. Z zestawu usunięto jeden temat, a następnie wylosowano z pozostałych jeden temat. Oblicz
tematów z prawdopodobieństwa. Z zestawu usunięto jeden temat, a następnie wylosowano z pozostałych jeden temat. Oblicz  , jeśli wiadomo, że prawdopodobieństwo wylosowania tematu z prawdopodobieństwa wynosi
, jeśli wiadomo, że prawdopodobieństwo wylosowania tematu z prawdopodobieństwa wynosi 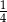 .
.
W pudełku znajdują się klocki o różnych kształtach i kolorach. Wiadomo, że prawdopodobieństwo wylosowania klocka, który ma kształt walca lub ma kolor czerwony jest równe 0,6. Prawdopodobieństwo, że losowo wybrany klocek czerwony jest walcem jest równe 0,25. Wiadomo też, że klocki czerwone stanowią 40% wszystkich klocków. Jakie jest prawdopodobieństwo, że losowo wybrany klocek w kształcie walca jest czerwony?

