/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 4 czerwca 2019 Czas pracy: 180 minut
Zadania zamknięte
Parametr 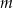 dobrano tak, że każda liczba rzeczywista jest rozwiązaniem równania
dobrano tak, że każda liczba rzeczywista jest rozwiązaniem równania
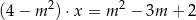
z niewiadomą  . Wynika stąd, że
. Wynika stąd, że
A) 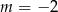 B)
B) 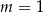 C)
C) 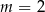 D)
D) 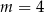
Dane są trzy niewspółliniowe punkty: 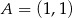 ,
, 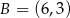 ,
, 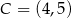 . Ile jest wszystkich punktów
. Ile jest wszystkich punktów 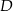 takich, że czworokąt o wierzchołkach w punktach
takich, że czworokąt o wierzchołkach w punktach 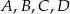 jest równoległobokiem?
jest równoległobokiem?
A) 1 B) 2 C) 3 D) 4
Wiadomo, że wielomian 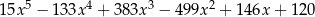 ma w zbiorze
ma w zbiorze 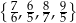 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A) 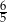 B)
B)  C)
C) 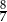 D)
D) 
Nieskończony ciąg geometryczny 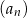 jest określony w następujący sposób:
jest określony w następujący sposób: 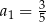 oraz
oraz 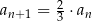 dla
dla 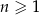 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 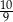 C)
C) 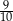 D)
D) 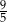
Zadania otwarte
W urnie znajduje się 16 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 10 kul białych i 6 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
Oblicz, ile jest siedmiocyfrowych liczb naturalnych takich, że iloczyn wszystkich ich cyfr w zapisie dziesiętnym jest równy 28.
Dana jest funkcja 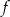 określona wzorem
określona wzorem 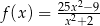 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz wartość
. Oblicz wartość 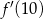 pochodnej tej funkcji dla argumentu 10.
pochodnej tej funkcji dla argumentu 10.
Dwusieczne kątów 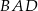 i
i 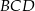 czworokąta wypukłego
czworokąta wypukłego 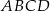 przecinają się w punkcie
przecinają się w punkcie 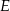 , przy czym punkty
, przy czym punkty 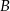 i
i 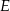 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 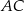 (zobacz rysunek).
(zobacz rysunek).
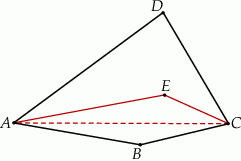
Wykaż, że 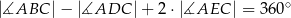 .
.
Udowodnij, że dla każdej liczby nieparzystej  wyrażenie
wyrażenie 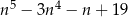 jest podzielne przez 16.
jest podzielne przez 16.
Miara kąta wewnętrznego  –kąta foremnego jest o
–kąta foremnego jest o 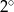 mniejsza od miary kąta wewnętrznego
mniejsza od miary kąta wewnętrznego 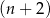 – kąta foremnego. Oblicz
– kąta foremnego. Oblicz  .
.
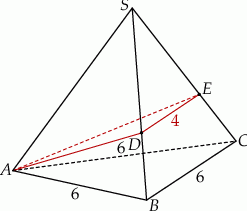
Podstawą ostrosłupa prawidłowego 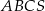 jest trójkąt równoboczny
jest trójkąt równoboczny 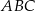 o boku długości 6. Na krawędziach bocznych
o boku długości 6. Na krawędziach bocznych 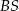 i
i 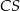 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio  i
i  , takie że
, takie że 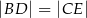 oraz
oraz 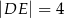 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 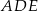 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 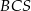 ostrosłupa.
ostrosłupa.
Wyznacz wszystkie wartości parametru 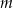 , dla których równanie
, dla których równanie
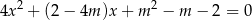
ma dwa różne dodatnie rozwiązania 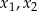 spełniające nierówność
spełniające nierówność 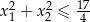 .
.
Punkt 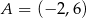 jest wierzchołkiem rombu
jest wierzchołkiem rombu 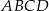 o polu 90. Przekątna
o polu 90. Przekątna 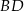 zawiera się w prostej
zawiera się w prostej 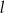 o równaniu
o równaniu 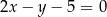 . Wyznacz długość boku tego rombu.
. Wyznacz długość boku tego rombu.
Rozwiąż równanie 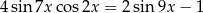 w przedziale
w przedziale 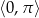 .
.
Dany jest okrąg o środku 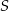 i promieniu 18. Rozpatrujemy pary okręgów: jeden o środku
i promieniu 18. Rozpatrujemy pary okręgów: jeden o środku 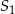 i promieniu
i promieniu  oraz drugi o środku
oraz drugi o środku 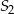 i promieniu
i promieniu 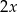 , o których wiadomo, że spełniają jednocześnie następujące warunki:
, o których wiadomo, że spełniają jednocześnie następujące warunki:
– rozważane dwa okręgi są styczne zewnętrznie;
– obydwa rozważane okręgi są styczne wewnętrznie do okręgu o środku 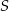 i promieniu 18;
i promieniu 18;
– punkty: 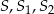 nie leżą na jednej prostej.
nie leżą na jednej prostej.
Pole trójkąta o bokach 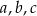 można obliczyć ze wzoru Herona
można obliczyć ze wzoru Herona
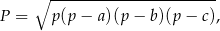
gdzie 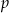 – jest połową obwodu trójkąta.
– jest połową obwodu trójkąta.
Zapisz pole trójkąta 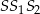 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.

