/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 16 marca 2013 Czas pracy: 180 minut
Narysuj w układzie współrzędnych zbiór
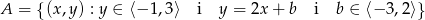
oraz oblicz jego pole powierzchni.
Uzasadnij, że 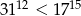 .
.
Wielomian 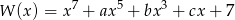 jest podzielny przez wielomian
jest podzielny przez wielomian 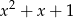 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 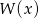 przez wielomian
przez wielomian 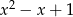 .
.
Rozwiąż nierówność 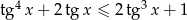 , gdzie
, gdzie 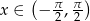 .
.
W półkole o promieniu  wpisano trapez równoramienny. Przekątna trapezu o długości
wpisano trapez równoramienny. Przekątna trapezu o długości 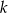 tworzy z dłuższą podstawą kąt o mierze
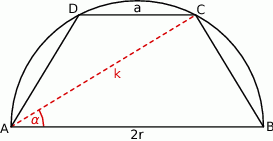
tworzy z dłuższą podstawą kąt o mierze  , a krótsza podstawa trapezu ma długość
, a krótsza podstawa trapezu ma długość  . Uzasadnij, że
. Uzasadnij, że 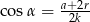 .
.
Dla jakich wartości parametru 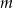 miejsca zerowe funkcji
miejsca zerowe funkcji 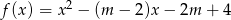 należą do przedziału
należą do przedziału 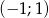 ?
?
Oblicz sumę wszystkich liczb naturalnych trzycyfrowych, które przy dzieleniu przez 7 dają resztę 5.
W układzie współrzędnych dane są punkty 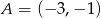 i
i 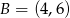 . Na wykresie funkcji
. Na wykresie funkcji 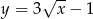 znajdź taki punkt
znajdź taki punkt 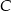 , dla którego pole trójkąta
, dla którego pole trójkąta 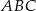 jest najmniejsze.
jest najmniejsze.
Podstawą ostrosłupa 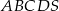 jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość
jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość 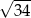 . Krawędź
. Krawędź 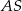 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 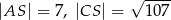 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Oblicz, ile jest liczb naturalnych pięciocyfrowych, których suma cyfr jest równa 5?

