/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 12 kwietnia 2014 Czas pracy: 180 minut
Dla jakich wartości parametru 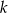 równanie
równanie 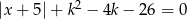 ma dwa pierwiastki różnych znaków?
ma dwa pierwiastki różnych znaków?
Reszta z dzielenia wielomianu 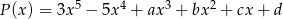 przez wielomian
przez wielomian 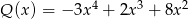 jest taka sama jak reszta z dzielenia wielomianu
jest taka sama jak reszta z dzielenia wielomianu 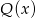 przez wielomian
przez wielomian 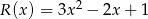 . Oblicz wartości współczynników
. Oblicz wartości współczynników 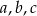 i
i 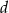 .
.
Dany jest czworokąt wypukły 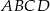 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 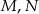 są odpowiednio środkami boków
są odpowiednio środkami boków 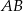 i
i 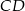 . Punkty
. Punkty 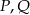 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 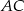 i
i 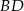 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 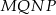 jest równoległobokiem.
jest równoległobokiem.
Wyznacz wszystkie wartości parametru 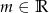 , dla których równanie
, dla których równanie 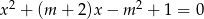 ma dwa różne pierwiastki
ma dwa różne pierwiastki 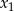 i
i 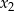 takie, że
takie, że 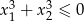 .
.
W trójkącie prostokątnym 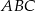 przyprostokątne mają długości
przyprostokątne mają długości 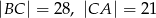 . Na boku
. Na boku 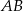 wybrano punkt
wybrano punkt 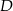 tak, że pole trójkąta
tak, że pole trójkąta 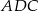 jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie
jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie 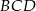 .
.
Rozwiąż równanie 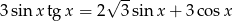 w przedziale
w przedziale 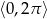 .
.
Oblicz jaka może być najmniejsza możliwa długość przeciwprostokątnej trójkąta prostokątnego o polu 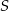 .
.
Oblicz, ile jest liczb naturalnych ośmiocyfrowych takich, że iloczyn cyfr w ich zapisie dziesiętnym jest równy 8.
Wyznacz wartość parametru 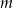 , dla której odległość punktu
, dla której odległość punktu 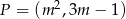 od prostej
od prostej 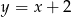 jest najmniejsza możliwa.
jest najmniejsza możliwa.
Podstawą ostrosłupa 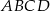 jest trójkąt równoramienny
jest trójkąt równoramienny 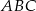 , w którym
, w którym 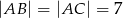 ,
, 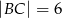 . Krawędzie boczne mają długości:
. Krawędzie boczne mają długości: 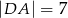 ,
, 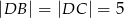 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Ciąg 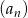 , gdzie
, gdzie 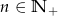 , określony jest następująco:
, określony jest następująco:
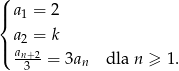
- Wyznacz wartość
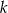 , jeżeli ciąg
, jeżeli ciąg 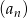 jest ciągiem geometrycznym, w którym suma sześciu początkowych wyrazów jest równa
jest ciągiem geometrycznym, w którym suma sześciu początkowych wyrazów jest równa 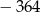 .
. - Oblicz, dla jakiej liczby
 suma
suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 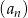 jest równa 9842.
jest równa 9842.
O zdarzeniach 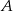 i
i 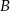 wiadomo, że
wiadomo, że 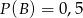 ;
; 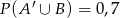 ;
; 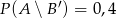 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 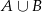 .
.

