/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 16 marca 2019 Czas pracy: 170 minut
Zadania zamknięte
Liczba 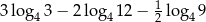 jest równa
jest równa
A) 4 B) 2 C) 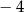 D)
D) 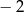
Liczba 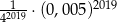 jest równa
jest równa
A) 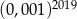 B)
B) 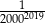 C)
C) 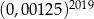 D)
D) 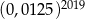
Liczbę 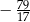 zaokrąglamy do najbliższej liczby całkowitej. Błąd bezwzględny tego przybliżenia jest równy
zaokrąglamy do najbliższej liczby całkowitej. Błąd bezwzględny tego przybliżenia jest równy
A) 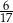 B)
B) 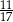 C)
C) 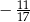 D)
D) 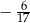
Cenę laptopa podwyższono o 12%, a następnie o 19%. W wyniku tych podwyżek cena laptopa wzrosła o 832 zł.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Przed podwyżkami ten laptop kosztował
A) 3332 zł B) 2500 zł C) 3000 zł D) 2375 zł
Największą liczbą całkowitą spełniającą nierówność 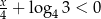 jest
jest
A) 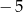 B)
B) 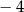 C)
C) 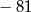 D)
D) 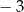
Równość 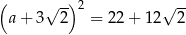 jest prawdziwa dla
jest prawdziwa dla
A) 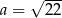 B)
B) 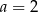 C)
C) 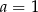 D)
D) 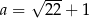
Liczbę 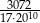 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. piętnastą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. piętnastą cyfrą po przecinku jego rozwinięcia jest
A) 6 B) 4 C) 7 D) 0
Rozwiązaniem równania 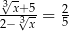 jest liczba
jest liczba
A) 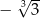 B)
B) 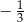 C)
C) 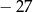 D)
D) 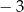
Wykresem funkcji kwadratowej 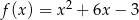 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 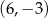 B)
B) 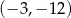 C)
C) 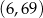 D)
D) 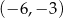
Rysunek przedstawia wykresy funkcji 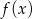 i
i 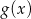 .
.
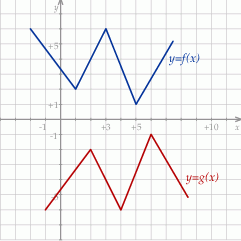
Prawdziwa jest równość:
A) 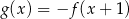 B)
B) 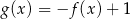
C) 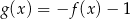 D)
D) 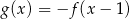
Funkcja liniowa 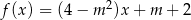 nie ma miejsc zerowych dla
nie ma miejsc zerowych dla
A) 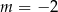 B)
B) 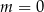 C)
C) 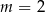 D)
D) 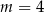
Największą wartością funkcji 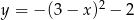 w przedziale
w przedziale 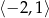 jest
jest
A) 2 B) 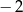 C)
C)  D)
D) 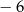
Dany jest ciąg geometryczny 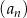 , określony dla
, określony dla 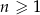 , w którym
, w którym 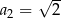 ,
, 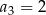 . Suma sześciu początkowych wyrazów ciągu
. Suma sześciu początkowych wyrazów ciągu 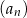 jest równa
jest równa
A) 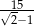 B)
B) 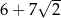 C)
C) 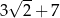 D)
D) 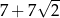
Ciąg arytmetyczny 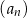 , określony dla
, określony dla 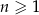 , spełnia warunek
, spełnia warunek 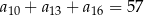 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 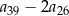 jest równa
jest równa
A) 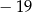 B)
B) 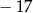 C) 13 D)
C) 13 D) 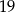
Trójka liczb 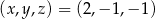 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 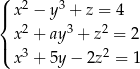 gdy
gdy
A) 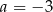 B)
B) 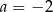 C)
C) 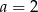 D)
D) 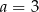
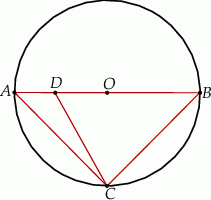
Odcinek 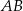 jest średnicą okręgu o środku
jest średnicą okręgu o środku 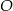 i promieniu
i promieniu  , a punkt
, a punkt 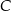 jest środkiem łuku o końcach
jest środkiem łuku o końcach 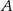 i
i 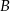 (zobacz rysunek). Na odcinku
(zobacz rysunek). Na odcinku 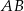 wybrano punkt
wybrano punkt 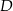 taki, że
taki, że 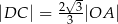 .
.
Pole trójkąta 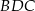 jest równe
jest równe
A) 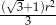 B)
B) 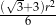 C)
C) 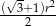 D)
D) 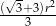
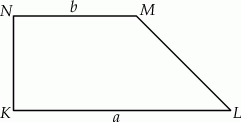
Dany jest trapez prostokątny 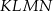 , którego podstawy mają długości
, którego podstawy mają długości 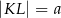 ,
, 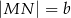 ,
, 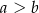 . Kąt
. Kąt 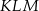 ma miarę
ma miarę 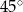 . Długość ramienia
. Długość ramienia 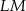 tego trapezu jest równa
tego trapezu jest równa
A) 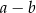 B)
B) 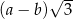 C)
C) 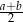 D)
D) 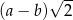
Jeżeli 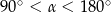 oraz
oraz 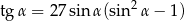 , to
, to
A) 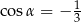 B)
B) 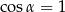 C)
C) 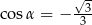 D)
D) 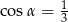
Miary kątów wewnętrznych pewnego pięciokąta pozostają w stosunku 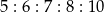 . Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
. Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
A) 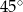 B)
B) 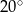 C)
C) 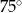 D)
D) 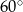
Proste o równaniach: 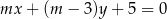 i
i 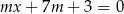 są równoległe, gdy
są równoległe, gdy
A) 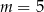 B)
B) 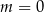 C)
C) 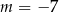 D)
D) 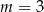
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 7 i 3. Kąt  , jaki przekątna tego graniastosłupa tworzy z jedną z krawędzi górnej podstawy jest równy
, jaki przekątna tego graniastosłupa tworzy z jedną z krawędzi górnej podstawy jest równy 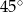 (zobacz rysunek).
(zobacz rysunek).
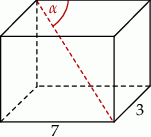
Wysokość graniastosłupa jest równa
A) 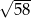 B)
B) 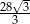 C)
C) 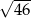 D)
D) 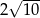
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 23 | 14 | 28 | 17 | 11 | 7 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o jedną książkę więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jednego ankietowanego mężczyznę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
Przekrój osiowy stożka jest trójkątem o polu 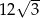 . Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem
. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 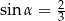 . Pole powierzchni bocznej tego stożka jest równe
. Pole powierzchni bocznej tego stożka jest równe
A) 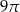 B)
B) 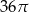 C)
C) 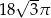 D)
D) 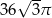
Punkty 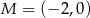 i
i 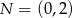 są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
A) 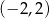 B)
B) 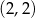 C)
C) 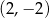 D)
D) 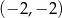
W pudełku jest 2400 kuponów, wśród których 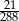 stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 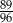 B)
B) 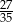 C)
C) 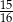 D)
D) 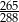
Zadania otwarte
Iloczyn pierwszego i czwartego wyrazu malejącego ciągu arytmetycznego 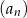 jest równy 253, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę pięć. Wyznacz różnicę tego ciągu.
jest równy 253, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę pięć. Wyznacz różnicę tego ciągu.
Wykresem funkcji kwadratowej 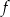 określonej wzorem
określonej wzorem 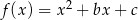 jest parabola, na której leży punkt
jest parabola, na której leży punkt 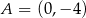 . Osią symetrii tej paraboli jest prosta o równaniu
. Osią symetrii tej paraboli jest prosta o równaniu 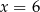 . Oblicz wartości współczynników
. Oblicz wartości współczynników 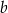 i
i  .
.
Dwa okręgi są zewnętrznie styczne w punkcie 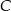 oraz są styczne do prostej
oraz są styczne do prostej 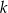 w punktach
w punktach 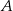 i
i 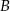 odpowiednio (zobacz rysunek).
odpowiednio (zobacz rysunek).
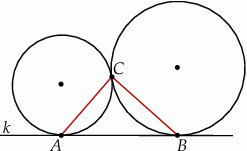
Uzasadnij, że trójkąt 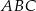 jest prostokątny.
jest prostokątny.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 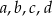 prawdziwa jest nierówność
prawdziwa jest nierówność
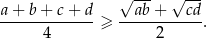
Kąt  jest ostry i
jest ostry i 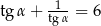 oblicz
oblicz 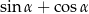 .
.
Okrąg o środku 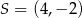 przechodzi przez punkt
przechodzi przez punkt 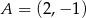 . Napisz równanie stycznej do tego okręgu przechodzącej przez punkt
. Napisz równanie stycznej do tego okręgu przechodzącej przez punkt 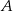 .
.
Dane są dwa zbiory:
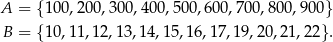
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 9.
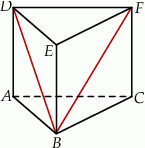
Podstawą graniastosłupa prostego 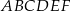 jest trójkąt
jest trójkąt 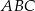 , w którym
, w którym 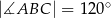 oraz
oraz 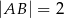 (zobacz rysunek). Trójkąt
(zobacz rysunek). Trójkąt 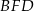 jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.
jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.
W trójkącie prostokątnym 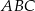 jedna z przyprostokątnych jest o 7 dłuższa od drugiej, a promień okręgu wpisanego w ten trójkąt jest równy 3. Oblicz obwód trójkąta
jedna z przyprostokątnych jest o 7 dłuższa od drugiej, a promień okręgu wpisanego w ten trójkąt jest równy 3. Oblicz obwód trójkąta 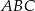 .
.

