/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 31 marca 2012 Czas pracy: 180 minut
Wyznacz wszystkie wartości parametru 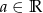 , dla których funkcja
, dla których funkcja 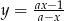 jest rosnąca w każdym przedziale, na którym jest określona. Dla
jest rosnąca w każdym przedziale, na którym jest określona. Dla 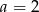 wyznacz zbiór wartości funkcji.
wyznacz zbiór wartości funkcji.
Liczby niezerowe 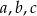 są wyrazami ciągu geometrycznego o numerach odpowiednio
są wyrazami ciągu geometrycznego o numerach odpowiednio 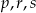 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
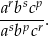
Boki prostokąta 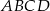 mają długości
mają długości 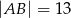 i
i 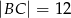 . Punkt
. Punkt 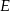 jest punktem boku
jest punktem boku 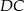 takim, że
takim, że 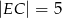 , a punkt
, a punkt 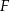 jest takim punktem odcinka
jest takim punktem odcinka 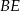 , że
, że 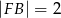 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 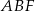 .
.
Uzasadnij, że dla dowolnej liczby naturalnej 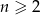 spełniona jest równość
spełniona jest równość
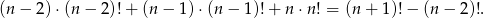
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
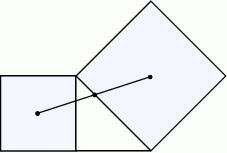
Wykaż, że jeżeli 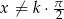 dla
dla 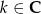 to prawdziwa jest tożsamość
to prawdziwa jest tożsamość
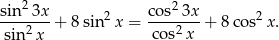
Wyznacz wszystkie wartości 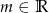 , dla których równanie
, dla których równanie 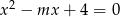 ma dwa różne pierwiastki spełniające nierówność
ma dwa różne pierwiastki spełniające nierówność 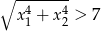 .
.
Dany jest trójkąt 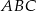 , w którym
, w którym 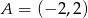 i
i 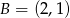 . Wierzchołek
. Wierzchołek 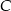 leży na prostej o równaniu
leży na prostej o równaniu 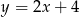 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 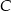 , dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
, dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
Wielomian 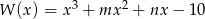 ma trzy pierwiastki
ma trzy pierwiastki 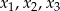 , przy czym
, przy czym 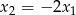 i
i 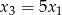 . Wyznacz
. Wyznacz 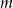 i
i  .
.
Podstawą ostrosłupa 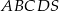 jest kwadrat
jest kwadrat 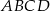 . Trójkąt równoramienny
. Trójkąt równoramienny 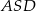 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 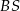 ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny
ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny 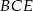 do płaszczyzny podstawy, gdzie
do płaszczyzny podstawy, gdzie 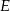 jest środkiem krawędzi
jest środkiem krawędzi 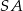 .
.
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 5.

