/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 25 kwietnia 2015 Czas pracy: 180 minut
Zadania zamknięte
Dany jest nieskończony ciąg geometryczny 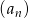 określony wzorem
określony wzorem 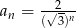 dla
dla 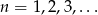 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A) 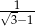 B)
B) 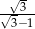 C)
C) 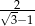 D)
D) 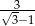
Ile miejsc zerowych ma funkcja 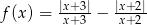 określona dla wszystkich liczb rzeczywistych
określona dla wszystkich liczb rzeczywistych  takich, że
takich, że 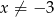 i
i 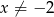 ?
?
A) 0 B) 1 C) 2 D) więcej niż 2
Jacek i Karol rzucają śnieżkami do celu. Jacek trafia do celu średnio trzy razy na dziesięć rzutów, a Karol trafia do celu średnio raz na pięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każdy z chłopców wykona po jednym rzucie jest równe
A) 0,06 B) 0,38 C) 0,56 D) 0,5
Okrąg o równaniu 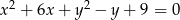 przekształcono w jednokładności o środku
przekształcono w jednokładności o środku 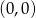 i skali
i skali 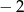 . Otrzymany okrąg ma równanie
. Otrzymany okrąg ma równanie
A) 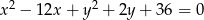
B) 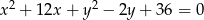
C) 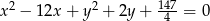
D) 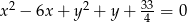
Liczba 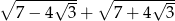 jest równa
jest równa
A) 16 B) 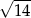 C) 4 D)
C) 4 D) 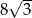
Zadania otwarte
Uzasadnij, że 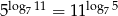 .
.
Dane są liczby 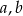 takie, że
takie, że 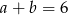 i
i 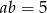 . Oblicz
. Oblicz 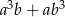 .
.
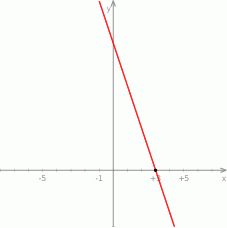
Na poniższym wykresie przedstawiono wykres pochodnej 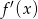 funkcji kwadratowej
funkcji kwadratowej 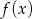 . Wykaż, że
. Wykaż, że 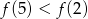 .
.
Oblicz granicę 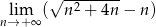 .
.
Wykaż, że 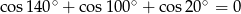 .
.
W trójkącie 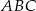 dane są:
dane są: 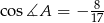 ,
, 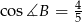 i
i 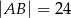 . Oblicz długości pozostałych boków trójkąta
. Oblicz długości pozostałych boków trójkąta 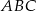 .
.
Dany jest ciąg 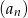 określony rekurencyjnie
określony rekurencyjnie
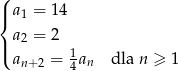
Oblicz sumę 18 początkowych wyrazów ciągu 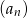 .
.
Uzasadnij, że wielomian 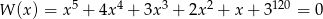 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych.
Wyznacz wszystkie wartości parametru 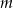 , dla których prosta
, dla których prosta 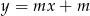 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 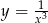 .
.
Rzucamy raz sześcienną kostką do gry, a następnie rzucamy tyloma monetami, ile oczek wypadło na kostce. Oblicz prawdopodobieństwo tego, że dokładnie na jednej z wyrzuconych monet jest reszka. Wynik podaj w postaci ułamka nieskracalnego.
Wyznacz wartość parametru 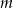 , dla której pole koła stycznego do prostych zawierających boki
, dla której pole koła stycznego do prostych zawierających boki 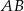 i
i 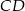 równoległoboku
równoległoboku 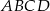 o wierzchołkach
o wierzchołkach 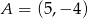 ,
, 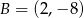 ,
, 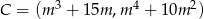 jest najmniejsze możliwe. Oblicz to pole.
jest najmniejsze możliwe. Oblicz to pole.
Wykaż, że jeżeli promień okręgu opisanego na trójkącie równoramiennym jest dwa razy dłuższy od promienia okręgu wpisanego w ten trójkąt, to trójkąt ten jest równoboczny.
W kulę o promieniu długości 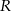 wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.

