/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 6 kwietnia 2019 Czas pracy: 180 minut
Zadania zamknięte
Niech 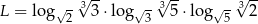 . Wtedy
. Wtedy
A) 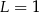 B)
B) 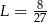 C)
C) 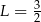 D)
D) 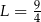
Na rysunku przedstawiono fragment wykresu funkcji 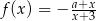 .
.
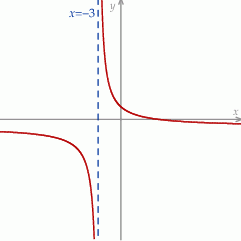
Liczba  może być równa
może być równa
A) 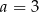 B)
B) 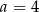 C)
C) 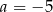 D)
D) 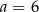
Jeżeli  jest takim kątem rozwartym, że
jest takim kątem rozwartym, że 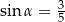 , to liczba
, to liczba 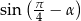 jest równa
jest równa
A) 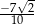 B)
B) 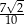 C)
C) 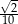 D)
D) 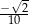
Granica 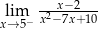 jest równa
jest równa
A) 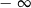 B)
B) 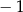 C) 0 D)
C) 0 D) 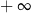
Funkcja 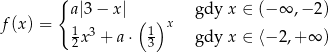 jest ciągła w zbiorze liczb rzeczywistych jeżeli
jest ciągła w zbiorze liczb rzeczywistych jeżeli  jest równe
jest równe
A) 1 B) 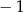 C)
C)  D)
D) 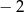
Oblicz współczynnik kierunkowy stycznej do wykresu funkcji 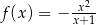 , określonej dla każdej liczby rzeczywistej
, określonej dla każdej liczby rzeczywistej 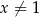 , poprowadzonej w punkcie
, poprowadzonej w punkcie 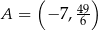 tego wykresu.
tego wykresu.
W kwadrat 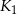 o boku
o boku  wpisujemy kwadrat
wpisujemy kwadrat 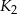 , którego wierzchołki są środkami boków kwadratu
, którego wierzchołki są środkami boków kwadratu 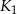 , następnie w kwadrat
, następnie w kwadrat 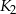 wpisujemy kwadrat
wpisujemy kwadrat 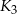 , którego wierzchołki są środkami boków
, którego wierzchołki są środkami boków 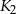 i tak dalej. Oblicz sumę pól otrzymanego w ten sposób nieskończonego ciągu kwadratów.
i tak dalej. Oblicz sumę pól otrzymanego w ten sposób nieskończonego ciągu kwadratów.
Na okręgu wybrano 50 punktów. Ile jest różnych czworokątów o wierzchołkach w tych punktach?
Dane są liczby całkowite  i
i 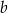 . Wykaż, że jeżeli liczba
. Wykaż, że jeżeli liczba 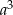 jest podzielna przez
jest podzielna przez 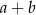 , to liczba
, to liczba 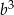 też jest podzielna
też jest podzielna 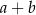 .
.
Wykaż, że dla dowolnej wartości parametru  równanie
równanie
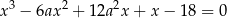
ma dokładnie jedno rozwiązanie rzeczywiste.
Ciąg 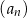 jest określony dla
jest określony dla 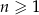 i spełnia warunki
i spełnia warunki
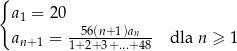
Oblicz granicę
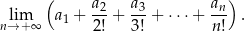
Rzucamy dziesięciokrotnie monetą. Wśród otrzymanych wyników dokładnie sześć razy otrzymaliśmy orła. Jakie jest prawdopodobieństwo, że w każdym z dwóch pierwszych rzutów otrzymaliśmy reszkę?
Przekątne trapezu 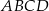 przecinają się w punkcie
przecinają się w punkcie 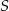 . Promień okręgu opisanego na trójkącie ostrokątnym
. Promień okręgu opisanego na trójkącie ostrokątnym 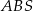 jest o 1 większy od promienia okręgu opisanego na trójkącie
jest o 1 większy od promienia okręgu opisanego na trójkącie 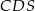 , a długości podstaw trapezu spełniają warunek
, a długości podstaw trapezu spełniają warunek 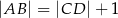 . Wykaż, że
. Wykaż, że
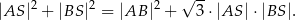
Rozwiąż równanie 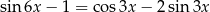 w przedziale
w przedziale 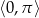 .
.
Wierzchołki 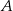 i
i 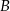 trójkąta prostokątnego
trójkąta prostokątnego 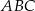 leżą na prostej
leżą na prostej 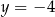 . Okrąg wpisany w ten trójkąt jest styczny do boków
. Okrąg wpisany w ten trójkąt jest styczny do boków 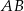 ,
, 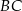 i
i 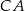 odpowiednio w punktach
odpowiednio w punktach 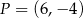 ,
, 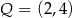 i
i 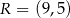 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 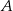 ,
, 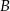 i
i 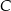 tego trójkąta.
tego trójkąta.
Podstawą ostrosłupa jest trójkąt prostokątny o kącie ostrym  i przeciwprostokątnej długości
i przeciwprostokątnej długości  . Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
. Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 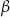 . Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe
. Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe 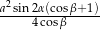 .
.
Rozważamy zbiór wszystkich trapezów równoramiennych, których krótsza podstawa i ramiona mają długość 6. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby jego pole było największe. Oblicz to pole.

