/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 11 marca 2017 Czas pracy: 170 minut
Zadania zamknięte
Dla każdej dodatniej liczby  iloraz
iloraz 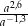 jest równy
jest równy
A) 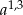 B)
B) 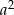 C)
C) 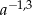 D)
D) 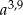
W prostopadłościanie o objętości 3400 skrócono o 10% najkrótsze krawędzie, a następnie wydłużono najdłuższe krawędzie tak, aby otrzymany prostopadłościan miał objętość 3519. O ile procent wydłużono najdłuższe krawędzie prostopadłościanu?
A) 18% B) 12% C) 15% D) 20%
Liczba dwa razy mniejsza od liczby 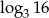 jest równa
jest równa
A) 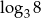 B)
B) 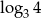 C)
C) 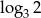 D)
D) 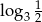
Różnica 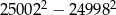 jest równa
jest równa
A) 2 000 000 B) 16 C) 200 000 D) 20 000
Jedną z liczb, które nie spełniają nierówność 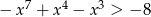 , jest
, jest
A) 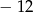 B)
B) 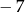 C) 20 D)
C) 20 D) 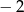
Funkcja kwadratowa określona jest wzorem 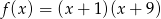 . Wynika stąd, że funkcja
. Wynika stąd, że funkcja 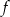 jest malejąca w przedziale
jest malejąca w przedziale
A) 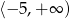 B)
B) 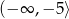 C)
C) 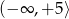 D)
D) 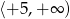
Największą liczbą całkowitą spełniającą nierówność 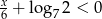 jest
jest
A) 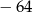 B)
B) 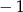 C)
C) 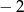 D)
D) 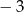
Na rysunku przedstawione są wykresy funkcji 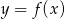 oraz
oraz 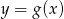 .
.
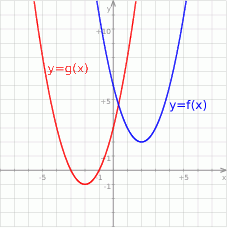
Wówczas :
A) 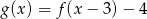
B) 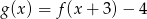
C) 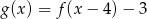
D) 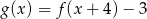
Równanie wymierne 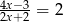 , gdzie
, gdzie 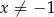 ,
,
A) ma dokładnie trzy rozwiązania rzeczywiste.
B) ma dokładnie dwa rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań rzeczywistych.
Funkcja 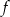 określona jest wzorem
określona jest wzorem 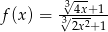 . Wtedy liczba
. Wtedy liczba 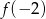 jest równa
jest równa
A) 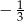 B)
B) 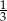 C) 0 D)
C) 0 D) 
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 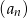 jest określona wzorem
jest określona wzorem 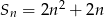 . Wtedy wyraz
. Wtedy wyraz 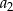 jest równy
jest równy
A) 4 B) 8 C) 12 D) 24
Dany jest trójkąt prostokątny o kątach ostrych  i
i 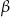 , w którym
, w którym 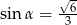 . Wtedy
. Wtedy
A) 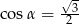 B)
B) 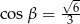 C)
C) 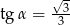 D)
D) 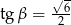
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 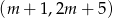 , gdzie
, gdzie 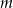 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 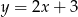 B)
B) 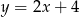 C)
C) 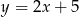 D)
D) 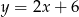
Dziewiąty wyraz ciągu geometrycznego jest równy 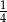 , a iloraz tego ciągu jest równy
, a iloraz tego ciągu jest równy 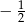 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 16 B) 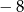 C)
C) 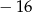 D) 8
D) 8
Punkty 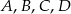 leżą na okręgu o środku
leżą na okręgu o środku 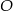 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
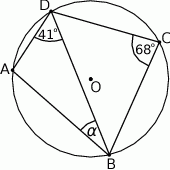
A) 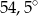 B)
B) 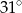 C)
C) 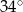 D)
D) 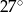
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia o dwa większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia o dwa większa. Objętość tego walca jest równa
A) 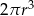 B)
B) 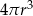 C)
C) 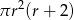 D)
D) 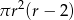
Punkty 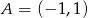 i
i 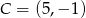 są wierzchołkami rombu
są wierzchołkami rombu 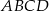 , a prosta określona równaniem
, a prosta określona równaniem 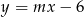 zawiera przekątną
zawiera przekątną 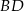 tego rombu. Wynika stąd, że
tego rombu. Wynika stąd, że
A) 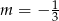 B)
B) 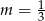 C)
C) 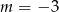 D)
D) 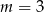
Z odcinków o długościach: 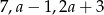 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 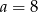 B)
B) 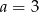 C)
C) 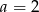 D)
D) 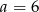
Przekątne trapezu 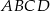 , w którym
, w którym 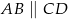 przecinają się w punkcie
przecinają się w punkcie 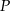 w ten sposób, że
w ten sposób, że 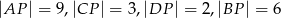 oraz
oraz 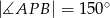 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe
A) 32 B) 24 C) 18 D) 16
Podstawą ostrosłupa prawidłowego czworokątnego 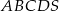 jest kwadrat
jest kwadrat 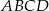 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta 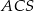 jest równa
jest równa
A) 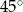 B)
B) 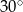 C)
C) 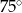 D)
D) 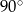
Liczb ze zbioru 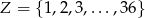 , których nie można uzyskać jako iloczynu dwóch niekoniecznie różnych liczb ze zbioru
, których nie można uzyskać jako iloczynu dwóch niekoniecznie różnych liczb ze zbioru 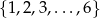 , jest
, jest
A) 8 B) 16 C) 18 D) 19
Rzucamy dziewięć razy symetryczną monetą. Niech 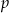 oznacza prawdopodobieństwo otrzymania co najwyżej 8 orłów w tych dziewięciu rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania co najwyżej 8 orłów w tych dziewięciu rzutach. Wtedy
A) 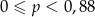 B)
B) 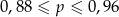 C)
C) 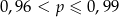 D)
D) 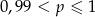
Punkt 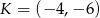 jest końcem odcinka
jest końcem odcinka 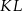 , punkt
, punkt 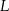 leży na osi
leży na osi 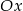 , a środek
, a środek 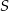 tego odcinka leży na osi
tego odcinka leży na osi 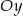 . Wynika stąd, że
. Wynika stąd, że
A) 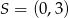 B)
B) 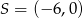 C)
C) 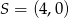 D)
D) 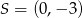
Dane są dwie sumy algebraiczne 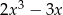 oraz
oraz 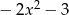 . Iloczyn tych sum jest równy
. Iloczyn tych sum jest równy
A) 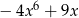 B)
B) 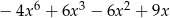 C)
C) 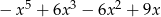 D)
D) 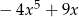
Zadania otwarte
W tabeli przedstawiono miesięczne sumy opadów w Terespolu w ciągu sześciu kolejnych miesięcy.
| Kolejne miesiące | 1 | 2 | 3 | 4 | 5 | 6 |
| Suma opadów (w mm) | 34 | 32 | 36 | 31 | 52 | 65 |
Oblicz średnią miesięczną wysokość opadów w Terespolu w badanym okresie sześciu miesięcy. Otrzymany wynik zaokrąglij z dokładnością do 1 mm. Oblicz błąd względny otrzymanego przybliżenia. Podaj ten błąd w procentach.
Rozwiąż równanie 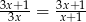 , gdzie
, gdzie 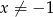 i
i 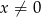 .
.
Suma długości przyprostokątnych trójkąta prostokątnego jest równa 7. Jaka jest najmniejsza możliwa długość przeciwprostokątnej tego trójkąta?
Ze zbioru ośmiu liczb naturalnych 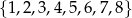 losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.
losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.
Ciąg 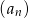 jest określony wzorem
jest określony wzorem 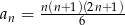 dla
dla 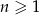 . Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
. Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
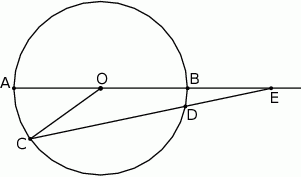
Średnica 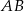 i cięciwa
i cięciwa 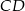 okręgu o środku
okręgu o środku 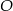 i promieniu
i promieniu  przecinają się w punkcie
przecinają się w punkcie 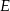 takim, że
takim, że 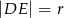 . Wykaż, że
. Wykaż, że 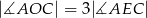 .
.
Wyznacz współrzędne środka okręgu opisanego na kwadracie, którego jeden z boków jest zawarty w prostej o równaniu 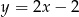 , a punkt
, a punkt 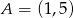 jest jego wierzchołkiem. Rozważ wszystkie przypadki.
jest jego wierzchołkiem. Rozważ wszystkie przypadki.
Podstawą ostrosłupa prawidłowego trójkątnego 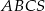 jest trójkąt równoboczny
jest trójkąt równoboczny 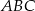 . Wysokość
. Wysokość 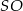 tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 8. Oblicz sumę długości wszystkich krawędzi ostrosłupa
tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 8. Oblicz sumę długości wszystkich krawędzi ostrosłupa 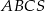 oraz cosinus kąta, jaki tworzą krawędź boczna i płaszczyzna podstawy ostrosłupa.
oraz cosinus kąta, jaki tworzą krawędź boczna i płaszczyzna podstawy ostrosłupa.
Pociąg pokonuje każdorazowo trasę pomiędzy Katowicami i Łodzią z taką samą zakładaną średnią prędkością. Pewnego dnia pociąg pokonał tę trasę w czasie o 10% krótszym od zakładanego, a następnego dnia w czasie o 15% dłuższym od zakładanego. Różnica prędkości średnich w tych dwóch dniach wyniosła 25 km/h. Ile wynosi zakładana średnia prędkość z jaką pociąg towarowy pokonuje trasę między Katowicami a Łodzią?

