/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez portal www.zadania.info poziom podstawowy 21 marca 2009 Czas pracy: 120 minut

Zadanie 1
(4 pkt)

Określ dziedzinę funkcji 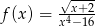√x-+2- f (x) = x4−16 .

Zadanie 2
(4 pkt)

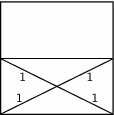
W kwadracie połączono odcinkiem środki przeciwległych boków. Wiedząc, że przekątne tak utworzonych prostokątów dzielą się na odcinki długości 1, oblicz pole wyjściowego kwadratu.

PIC

Zadanie 3
(5 pkt)

Na podanym wykresie przedstawiono stan wody

PIC

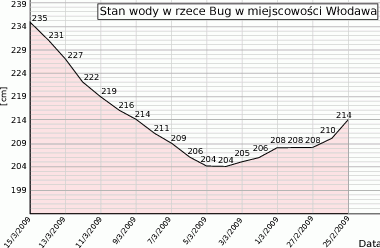
w rzece Bug w okresie od 25 lutego do 15 marca 2009.

  • W których dniach stan wody w rzece nie przekraczał 207 cm?
  • Jaki był średni stan wody w rzece w dniach 1-10 marca 2009?
  • O ile procent podniósł się stan wody w rzece między 6 a 12 marca? Wynik podaj z dokładnością do jednego punktu procentowego.

Zadanie 4
(4 pkt)

Wyznacz takie dwie liczby o sumie 100, których suma kwadratów jest najmniejsza.

Zadanie 5
(5 pkt)

Z danego wykresu funkcji 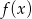f(x) odczytaj

PIC

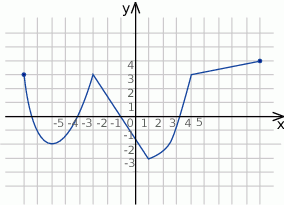
  • zbiór wartości funkcji f (x) ;
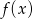  • rozwiązania równania f(x ) = 3 ;
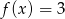  • maksymalne przedziały monotoniczności funkcji f (x) .

Zadanie 6
(3 pkt)

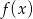Cena brutto aparatu fotograficznego powstaje z jego ceny netto przez dodanie 22% podatku VAT. O ile należy zwiększyć cenę netto aparatu, aby cena brutto wzrosła o 10 zł? Wynik podaj z dokładnością do 1 grosza.

Zadanie 7
(4 pkt)

Rysunek przedstawia kształt obszaru zakreślanego przez wycieraczkę samochodową.

PIC

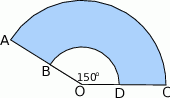
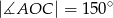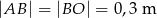Wiedząc, że |∡AOC | = 150∘ oraz |AB | = |BO | = 0,3 m oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że 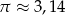π ≈ 3 ,14 podaj wynik z dokładnością do 0 ,01 m .

Zadanie 8
(5 pkt)

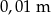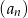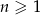Ciąg (an) , dla n ≥ 1 jest ciągiem geometrycznym o ilorazie 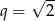√ -- q = 2 . Oblicz wartość wyrażenia

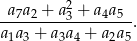
a7a2 + a2+ a4a5 ---------3--------. a1a3 + a3a4 + a2a5

Zadanie 9
(4 pkt)

Napisz równanie wysokości trójkąta o wierzchołkach 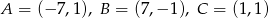A = (− 7,1), B = (7,− 1), C = (1,1) opuszczonej z wierzchołka A .

Zadanie 10
(4 pkt)

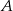Oblicz prawdopodobieństwo, że losowo wybrana liczba trzycyfrowa ma wszystkie cyfry różne.

Zadanie 11
(5 pkt)

Oblicz objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy 6 cm i krawędzi bocznej 12 cm.

Zadanie 12
(3 pkt)

Rozwiąż równanie 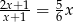2x+-1 5 x+1 = 6x .

Arkusz Wersja PDF
Rozwiązania