/Szkoła średnia/Zadania maturalne

Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony
(stara formuła) 5 czerwca 2018 Czas pracy: 180 minut

Zadanie 1

(4 pkt)

Rozwiąż nierówność 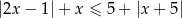|2x − 1|+ x ≤ 5 + |x + 5| .

Zadanie 2

(5 pkt)

Rozwiąż równanie 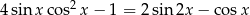4 sinx cos2 x− 1 = 2sin 2x − cos x w przedziale (0,2 π) .

Zadanie 3

(5 pkt)

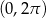Podstawą ostrosłupa prawidłowego 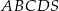ABCDS jest kwadrat 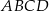ABCD . Punkt 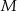jest środkiem odcinka 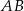, a punkt 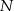jest środkiem odcinka 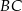. Trójkąt 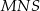MNS jest równoboczny i jego bok ma długość 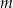. Oblicz objętość ostrosłupa 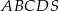ABCDS i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.

Zadanie 4

(4 pkt)

Dany jest rosnący ciąg geometryczny 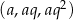(a,aq,aq 2) , którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 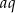tego ciągu.

Zadanie 5

(3 pkt)

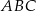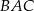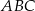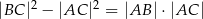W trójkącie ABC kąt BAC jest dwa razy większy od kąta ABC . Wykaż, że prawdziwa jest równość 2 2 |BC | − |AC | = |AB |⋅|AC | .

Zadanie 6

(3 pkt)

Dodatnie liczby rzeczywiste i 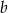takie, że 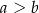a > b , spełniają warunek

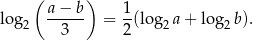
( a − b) 1 log 2 ------ = --(lo g2a + log2 b). 3 2

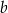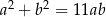Wykaż, że dla liczb i prawdziwa jest równość 2 2 a + b = 11ab .

Zadanie 7

(4 pkt)

Ze zbioru wszystkich liczb naturalnych ośmiocyfrowych, w których zapisie dziesiętnym występują tylko cyfry ze zbioru 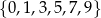{0,1,3 ,5 ,7,9} , losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma cyfr wylosowanej liczby jest równa 3.

Zadanie 8

(5 pkt)

Trapez prostokątny 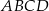ABCD o podstawach 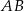i 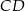jest opisany na okręgu. Ramię 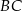ma długość 10, a ramię 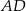jest wysokością trapezu. Podstawa 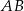jest 2 razy dłuższa od podstawy 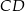. Oblicz pole tego trapezu.

Zadanie 9

(6 pkt)

Wyznacz wszystkie wartości parametru 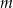, dla których równanie

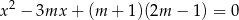
2 x − 3mx + (m + 1)(2m − 1) = 0

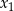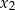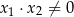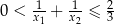ma dwa różne rozwiązania , spełniające warunki: x 1 ⋅x 2 ⁄= 0 oraz 0 < 1-+ 1-≤ 2 x1 x2 3 .

Zadanie 10

(6 pkt)

Wielomian 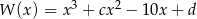W (x) = x3 + cx2 − 10x + d jest podzielny przez dwumian 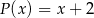P (x) = x + 2 . Przy dzieleniu wielomianu 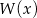W (x) przez dwumian 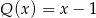Q (x) = x − 1 otrzymujemy resztę 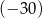(− 30) . Oblicz pierwiastki wielomianu 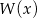W (x) i rozwiąż nierówność W (x) ≥ 0 .

Zadanie 11

(5 pkt)

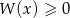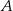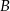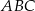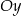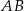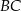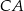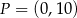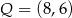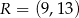Wierzchołki i trójkąta prostokątnego ABC leżą na osi układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków , i w punktach – odpowiednio – P = (0,10) , Q = (8 ,6) i R = (9,1 3) . Oblicz współrzędne wierzchołków 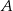, 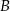i 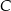tego trójkąta.