/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 12 kwietnia 2014 Czas pracy: 170 minut
Zadania zamknięte
Liczba 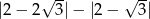 jest równa
jest równa
A) 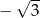 B)
B) 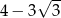 C)
C) 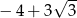 D)
D) 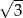
Liczby  i
i 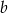 są dodatnie oraz 28% liczby
są dodatnie oraz 28% liczby  jest równe 49% liczby
jest równe 49% liczby 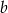 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 57% liczby 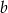 B) 125% liczby
B) 125% liczby 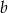 C) 175% liczby
C) 175% liczby 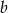 D) 149% liczby
D) 149% liczby 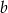
Liczba 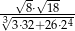 jest równa
jest równa
A)  B)
B)  C) 2 D) 3
C) 2 D) 3
Układem sprzecznym jest układ
A) 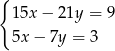 B)
B) 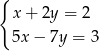 C)
C) 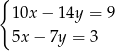 D)
D) 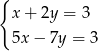
Wykres funkcji liniowej 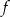 przecina osie układu współrzędnych w punktach
przecina osie układu współrzędnych w punktach 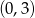 i
i 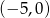 . Wynika stąd, że
. Wynika stąd, że
A) 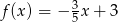 B)
B) 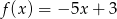 C)
C) 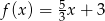 D)
D) 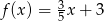
Punkt 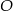 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
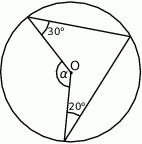
A) 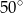 B)
B) 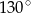 C)
C) 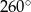 D)
D) 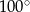
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 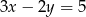 jest równy
jest równy
A) 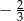 B)
B)  C)
C)  D)
D) 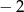
Wskaż postać kanoniczną trójmianu 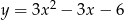 .
.
A) 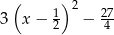 B)
B) 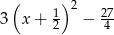 C)
C) 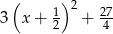 D)
D) 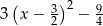
Kilka początkowych wyrazów ciągu geometrycznego 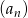 to:
to: 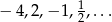 . Wyraz
. Wyraz 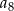 tego ciągu jest równy
tego ciągu jest równy
A) 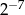 B)
B) 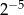 C)
C) 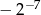 D)
D) 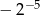
Na rysunku 1 jest przedstawiony wykres funkcji 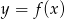 .
.
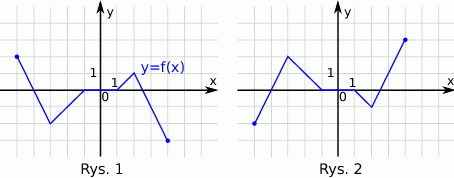
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 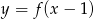 B)
B) 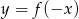 C)
C) 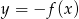 D)
D) 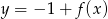
Wielomian 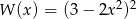 jest równy wielomianowi
jest równy wielomianowi
A) 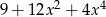 B)
B) 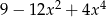 C)
C) 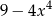 D)
D) 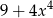
Rozwiązaniem równania 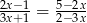 jest
jest
A) 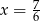 B)
B) 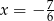 C)
C) 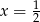 D)
D) 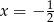
Obwód prostokąta jest równy 36 cm, a jeden z jego boków jest 5 razy dłuższy od drugiego boku. Pole tego prostokąta jest równe:
A) 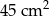 B)
B) 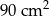 C)
C) 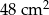 D)
D) 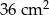
Wyrażenie 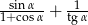 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 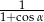 B)
B) 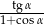 C)
C) 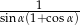 D)
D) 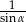
Liczb czterocyfrowych o jednakowej cyfrze setek i jedności jest
A) 9000 B) 3000 C) 900 D) 28
Cięciwa okręgu ma długość 6 cm i jest oddalona od jego środka o 2 cm. Pole koła ograniczonego tym okręgiem jest równe
A) 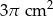 B)
B) 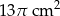 C)
C) 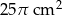 D)
D) 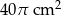
Ile różnych pierwiastków ma wielomian 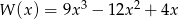 ?
?
A) 0 B) 1 C) 2 D) 3
Punkty 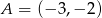 i
i 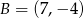 są dwoma sąsiednimi wierzchołkami rombu
są dwoma sąsiednimi wierzchołkami rombu 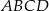 . Obwód tego rombu jest równy
. Obwód tego rombu jest równy
A) 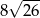 B)
B) 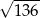 C)
C) 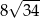 D)
D) 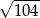
Liczba wszystkich krawędzi graniastosłupa jest równa 21. Wówczas podstawą tego graniastosłupa jest:
A) sześciokąt B) ośmiokąt C) siedmiokąt D) dwunastokąt
Cztery liczby dodatnie 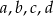 w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby
w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby 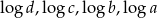 (w podanej kolejności) tworzą
(w podanej kolejności) tworzą
A) ciąg geometryczny o ilorazie 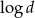
B) ciąg arytmetyczny o różnicy 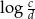
C) ciąg arytmetyczny o różnicy 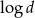
D) ciąg arytmetyczny o różnicy 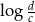
Mediana uporządkowanego niemalejąco zestawu liczb: 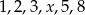 nie zmienia się po dopisaniu liczby 10. Wtedy
nie zmienia się po dopisaniu liczby 10. Wtedy
A) 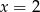 B)
B) 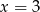 C)
C) 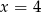 D)
D) 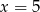
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo otrzymania co najmniej raz pięciu oczek jest równe
A) 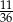 B)
B) 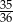 C)
C) 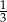 D)
D) 
Objętość stożka o wysokości 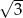 i kącie rozwarcia
i kącie rozwarcia 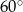 jest równa
jest równa
A) 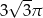 B)
B) 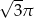 C)
C) 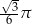 D)
D) 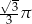
Liczba 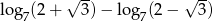 jest równa
jest równa
A) 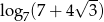 B)
B) 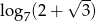 C) 0 D)
C) 0 D) 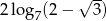
Zadania otwarte
Udowodnij, że jeżeli liczby 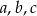 są kolejnymi wyrazami ciągu geometrycznego, to
są kolejnymi wyrazami ciągu geometrycznego, to
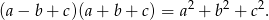
Rozwiąż równanie 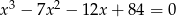 .
.
Kąt  jest ostry i
jest ostry i 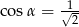 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 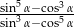 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 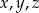 takich, że
takich, że 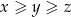 , prawdziwa jest nierówność
, prawdziwa jest nierówność
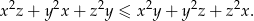
Możesz skorzystać z tożsamości
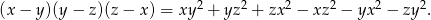
Po wydłużeniu każdej krawędzi sześcianu o 2, długość jego przekątnej podwoiła się. Oblicz pole powierzchni całkowitej powiększonego sześcianu.
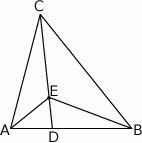
Na boku 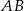 trójkąta
trójkąta 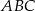 wybrano punkt
wybrano punkt 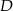 , a na odcinku
, a na odcinku 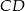 wybrano punkt
wybrano punkt 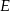 . Wykaż, że stosunek pól trójkątów
. Wykaż, że stosunek pól trójkątów 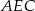 i
i 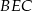 jest równy stosunkowi pól trójkątów
jest równy stosunkowi pól trójkątów 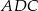 i
i 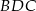 .
.
Oblicz sumę wszystkich liczb naturalnych trzycyfrowych, które przy dzieleniu przez 8 dają resztę 3.
Z metalowej rury wycięto dwa walce o tym samym promieniu podstawy. Objętość pierwszego z walców jest równa 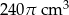 , a drugi walec jest wyższy od pierwszego o
, a drugi walec jest wyższy od pierwszego o 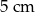 i ma objętość większą o
i ma objętość większą o 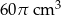 . Oblicz wysokości obu walców.
. Oblicz wysokości obu walców.
Wierzchołki trójkąta 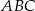 mają współrzędne:
mają współrzędne: 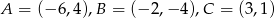 . Napisz równanie okręgu, który jest styczny do prostej
. Napisz równanie okręgu, który jest styczny do prostej 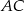 , a jego środek jest punktem przecięcia się wysokości trójkąta
, a jego środek jest punktem przecięcia się wysokości trójkąta 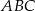 .
.

