/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom podstawowy 7 maja 2019 Czas pracy: 170 minut
Zadania zamknięte
Liczba 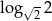 jest równa
jest równa
A) 2 B) 4 C) 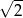 D)
D) 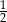
Liczba naturalna 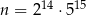 w zapisie dziesiętnym ma
w zapisie dziesiętnym ma
A) 14 cyfr B) 15 cyfr C) 16 cyfr D) 30 cyfr
W pewnym banku prowizja od udzielanych kredytów hipotecznych przez cały styczeń była równa 4%. Na początku lutego ten bank obniżył wysokość prowizji od wszystkich kredytów o 1 punkt procentowy. Oznacza to, że prowizja od kredytów hipotecznych w tym banku zmniejszyła się o
A) 1% B) 25% C) 33% D) 75%
Równość 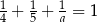 jest prawdziwa dla
jest prawdziwa dla
A) 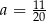 B)
B) 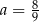 C)
C) 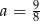 D)
D) 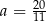
Para liczb 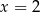 i
i 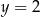 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 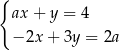 dla
dla
A) 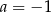 B)
B) 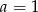 C)
C) 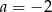 D)
D) 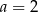
Równanie 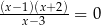
A) ma trzy różne rozwiązania: 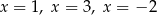 .
.
B) ma trzy różne rozwiązania: 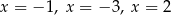 .
.
C) ma dwa różne rozwiązania: 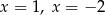 .
.
D) ma dwa różne rozwiązania: 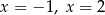 .
.
Miejscem zerowym funkcji liniowej 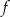 określonej wzorem
określonej wzorem 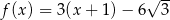 jest liczba
jest liczba
A) 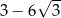 B)
B) 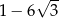 C)
C) 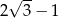 D)
D) 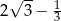
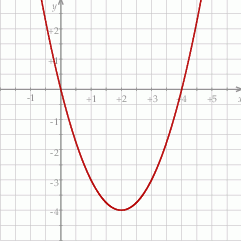
Informacja do zadań 8 – 10
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 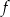 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 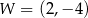 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 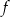 .
.
Zbiorem wartości funkcji 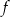 jest przedział
jest przedział
A) 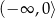 B)
B) 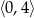 C)
C) 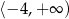 D)
D) 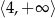
Największa wartość funkcji 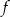 w przedziale
w przedziale 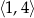 jest równa
jest równa
A) 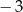 B)
B) 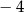 C) 4 D) 0
C) 4 D) 0
Osią symetrii wykresu funkcji 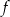 jest prosta o równaniu
jest prosta o równaniu
A) 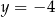 B)
B) 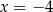 C)
C) 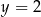 D)
D) 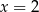
W ciągu arytmetycznym 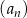 , określonym dla
, określonym dla 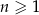 , dane są dwa wyrazy:
, dane są dwa wyrazy: 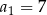 oraz
oraz 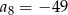 . Suma ośmiu początkowych wyrazów tego ciągu jest równa
. Suma ośmiu początkowych wyrazów tego ciągu jest równa
A) 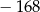 B)
B) 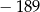 C)
C) 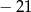 D)
D) 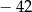
Dany jest ciąg geometryczny 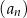 , określony dla
, określony dla 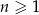 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 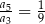 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 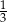 B)
B) 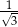 C) 3 D)
C) 3 D) 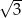
Sinus kąta ostrego  jest równy
jest równy  . Wtedy
. Wtedy
A) 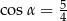 B)
B) 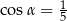 C)
C) 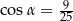 D)
D) 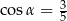
Punkty 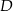 i
i 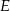 leżą na okręgu opisanym na trójkącie równobocznym
leżą na okręgu opisanym na trójkącie równobocznym 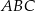 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 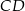 jest średnicą tego okręgu. Kąt wpisany
jest średnicą tego okręgu. Kąt wpisany 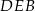 ma miarę
ma miarę  .
.
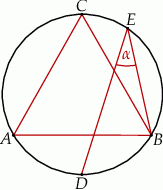
Zatem
A) 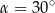 B)
B) 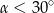 C)
C) 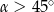 D)
D) 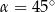
Dane są dwa okręgi: okrąg o środku w punkcie 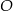 i promieniu 5 oraz okrąg o środku w punkcie
i promieniu 5 oraz okrąg o środku w punkcie 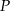 i promieniu 3. Odcinek
i promieniu 3. Odcinek 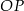 ma długość 16. Prosta
ma długość 16. Prosta 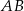 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 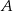 i
i 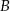 . Ponadto prosta
. Ponadto prosta 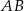 przecina odcinek
przecina odcinek 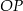 w punkcie
w punkcie  (zobacz rysunek).
(zobacz rysunek).
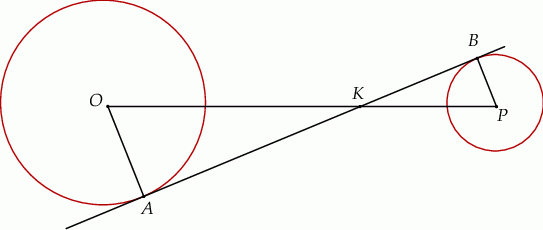
Wtedy
A) 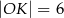 B)
B) 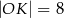 C)
C) 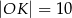 D)
D) 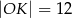
Dany jest romb o boku długości 4 i kącie rozwartym 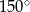 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 8 B) 12 C) 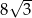 D) 16
D) 16
Proste o równaniach 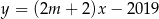 i
i 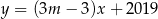 są równoległe, gdy
są równoległe, gdy
A) 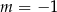 B)
B) 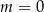 C)
C) 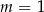 D)
D) 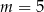
Prosta o równaniu 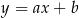 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 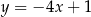 i przechodzi przez punkt
i przechodzi przez punkt 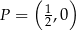 , gdy
, gdy
A) 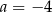 i
i 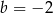 B)
B) 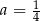 i
i 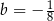
C) 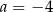 i
i 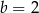 D)
D) 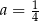 i
i 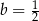
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 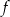 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 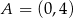 i
i 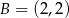 .
.
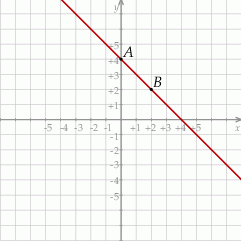
Obrazem prostej 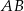 w symetrii względem początku układu współrzędnych jest wykres funkcji
w symetrii względem początku układu współrzędnych jest wykres funkcji 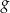 określonej wzorem
określonej wzorem
A) 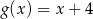 B)
B) 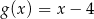 C)
C) 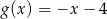 D)
D) 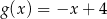
Dane są punkty o współrzędnych 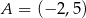 oraz
oraz 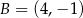 . Średnica okręgu wpisanego w kwadrat o boku
. Średnica okręgu wpisanego w kwadrat o boku 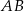 jest równa
jest równa
A) 12 B) 6 C) 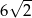 D)
D) 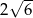
Pudełko w kształcie prostopadłościanu ma wymiary 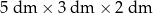 (zobacz rysunek).
(zobacz rysunek).
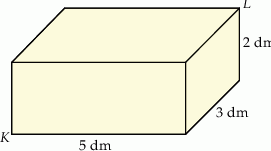
Przekątna 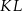 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 5,83 dm B) 6,16 dm C) 3,61 dm D) 5,39 dm
Promień kuli i promień podstawy stożka są równe 4. Pole powierzchni kuli jest równe polu powierzchni całkowitej stożka. Długość tworzącej stożka jest równa
A) 8 B) 4 C) 16 D) 12
Mediana zestawu sześciu danych liczb: 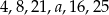 jest równa 14. Zatem
jest równa 14. Zatem
A) 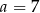 B)
B) 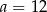 C)
C) 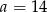 D)
D) 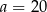
Wszystkich liczb pięciocyfrowych, w których występują wyłącznie cyfry 0, 2, 5, jest
A) 12 B) 36 C) 162 D) 243
W pudełku jest 40 kul. Wśród nich jest 35 kul białych, a pozostałe to kule czerwone. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę czerwoną, jest równe
A)  B)
B) 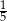 C)
C) 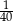 D)
D) 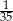
Zadania otwarte
Rozwiąż równanie 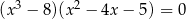 .
.
Rozwiąż nierówność 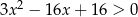 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 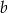 prawdziwa jest nierówność
prawdziwa jest nierówność
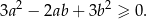
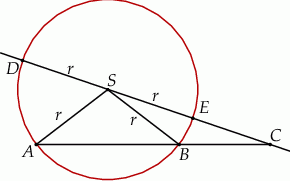
Dany jest okrąg o środku w punkcie 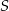 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 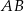 poza punkt
poza punkt 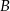 odłożono odcinek
odłożono odcinek 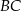 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 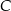 i
i 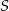 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 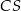 przecina dany okrąg w punktach
przecina dany okrąg w punktach 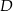 i
i 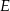 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 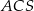 jest równa
jest równa  , to miara kąta
, to miara kąta 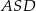 jest równa
jest równa 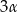 .
.
Ze zbioru liczb 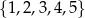 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 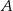 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
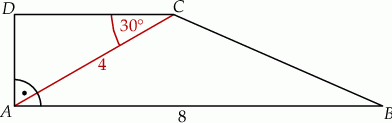
W trapezie prostokątnym 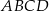 dłuższa podstawa
dłuższa podstawa 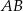 ma długość 8. Przekątna
ma długość 8. Przekątna 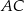 tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze
tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze 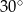 (zobacz rysunek). Oblicz długość przekątnej
(zobacz rysunek). Oblicz długość przekątnej 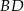 tego trapezu.
tego trapezu.
Ciąg arytmetyczny 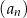 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 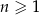 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba 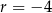 , a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu:
, a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu: 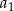 ,
, 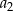 ,
, 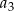 ,
, 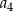 ,
, 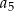 ,
, 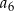 , jest równa 16.
, jest równa 16.
- Oblicz pierwszy wyraz tego ciągu.
- Oblicz liczbę
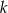 , dla której
, dla której 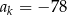 .
.
Dany jest punkt 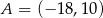 . Prosta o równaniu
. Prosta o równaniu 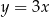 jest symetralną odcinka
jest symetralną odcinka 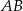 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 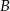 .
.
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa 6. Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt  jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta
jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta  .
.