/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony
(stara formuła) 4 czerwca 2019 Czas pracy: 180 minut
Funkcja 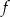 jest określona wzorem
jest określona wzorem 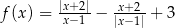 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 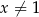 . Wyznacz zbiór jej wartości.
. Wyznacz zbiór jej wartości.
Dwusieczne kątów 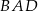 i
i 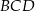 czworokąta wypukłego
czworokąta wypukłego 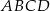 przecinają się w punkcie
przecinają się w punkcie 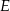 , przy czym punkty
, przy czym punkty 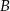 i
i 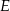 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 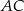 (zobacz rysunek).
(zobacz rysunek).
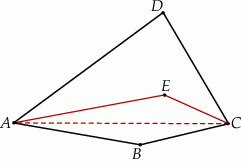
Wykaż, że 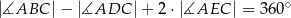 .
.
Udowodnij, że dla każdej liczby nieparzystej  wyrażenie
wyrażenie 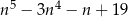 jest podzielne przez 16.
jest podzielne przez 16.
W ciągu geometrycznym 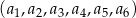 suma wyrazów o numerach nieparzystych jest równa 182, a stosunek sumy wyrazów o numerach nieparzystych do sumy wyrazów o numerach parzystych jest równy
suma wyrazów o numerach nieparzystych jest równa 182, a stosunek sumy wyrazów o numerach nieparzystych do sumy wyrazów o numerach parzystych jest równy 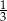 . Wyznacz wszystkie wyrazy tego ciągu.
. Wyznacz wszystkie wyrazy tego ciągu.
Punkt 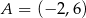 jest wierzchołkiem rombu
jest wierzchołkiem rombu 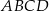 o polu 90. Przekątna
o polu 90. Przekątna 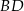 zawiera się w prostej
zawiera się w prostej 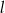 o równaniu
o równaniu 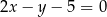 . Wyznacz długość boku tego rombu.
. Wyznacz długość boku tego rombu.
Wyznacz najmniejszą liczbę całkowitą spełniającą nierówność
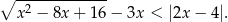
Wyznacz wszystkie rozwiązania równania 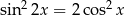 należące do przedziału
należące do przedziału 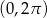 .
.
Miara kąta wewnętrznego  –kąta foremnego jest o
–kąta foremnego jest o 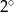 mniejsza od miary kąta wewnętrznego
mniejsza od miary kąta wewnętrznego 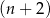 – kąta foremnego. Oblicz
– kąta foremnego. Oblicz  .
.
Wyznacz wszystkie wartości parametru 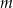 , dla których równanie
, dla których równanie
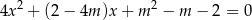
ma dwa różne dodatnie rozwiązania 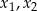 spełniające nierówność
spełniające nierówność 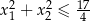 .
.
W urnie jest dziesięć kul różniących się wyłącznie kolorem: 4 czarne, 3 białe, 2 zielone i 1 niebieska. Losujemy jednocześnie trzy kule z urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przynajmniej dwie z wylosowanych kul mają ten sam kolor.
Podstawą ostrosłupa prawidłowego 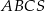 jest trójkąt równoboczny
jest trójkąt równoboczny 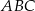 o boku długości 6. Na krawędziach bocznych
o boku długości 6. Na krawędziach bocznych 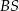 i
i 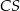 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 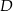 i
i 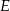 , takie że
, takie że 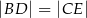 oraz
oraz 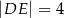 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 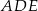 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 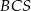 ostrosłupa.
ostrosłupa.