/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 25 marca 2017 Czas pracy: 180 minut
Zadania zamknięte
Wyrażenie 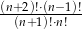 dla liczby naturalnej
dla liczby naturalnej 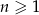 jest równe
jest równe
A) 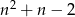 B)
B) 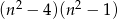 C)
C) 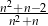 D)
D) 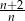
Wartość wyrażenia 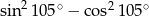 jest równa
jest równa
A) 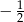 B)
B) 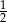 C)
C) 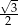 D)
D) 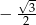
Ile jest liczb naturalnych dwudziestocyfrowych, których iloczyn cyfr jest równy 25?
A) 380 B) 190 C) 250 D) 500
Pochodna 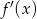 funkcji
funkcji 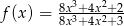 jest określona wzorem
jest określona wzorem
A) 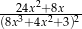 B)
B) 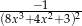 C)
C) 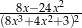 D)
D) 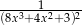
Dana jest funkcja 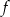 określona wzorem
określona wzorem 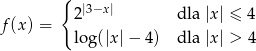
Równanie 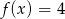 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) trzy rozwiązania. D) cztery rozwiązania.
Zadania otwarte
Dane są zdarzenia losowe 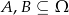 takie, że
takie, że 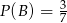 i
i 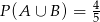 . Oblicz
. Oblicz 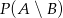 , gdzie zdarzenie
, gdzie zdarzenie 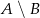 oznacza różnicę zdarzeń
oznacza różnicę zdarzeń 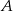 i
i 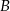 .
.
Oblicz granicę 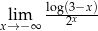 .
.
W każdej z dwóch szuflad jest tyle samo rękawiczek prawych i lewych, a trzecia szuflada jest pusta. Z każdej z dwóch pierwszych szuflad losujemy jedną rękawiczkę i wkładamy je do trzeciej szuflady. Następnie z trzeciej szuflady losujemy jedną rękawiczkę. Oblicz prawdopodobieństwo tego, że rękawiczka wylosowana z trzeciej szuflady jest lewa.
Dany jest prostopadłościan 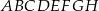 . Przez wierzchołki
. Przez wierzchołki 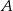 i
i 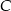 oraz środek
oraz środek 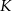 krawędzi
krawędzi 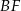 poprowadzono płaszczyznę, która przecina przekątną
poprowadzono płaszczyznę, która przecina przekątną 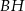 w punkcie
w punkcie 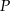 (zobacz rysunek).
(zobacz rysunek).
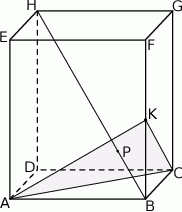
Oblicz 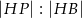 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 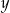 takich, że
takich, że 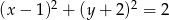 , prawdziwa jest nierówność
, prawdziwa jest nierówność 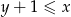 .
.
Ciąg 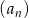 jest określony dla
jest określony dla 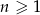 i spełnia warunki
i spełnia warunki
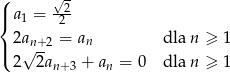
Oblicz granicę
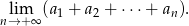
Rozwiąż nierówność 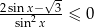 w przedziale
w przedziale 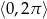 .
.
W trójkącie prostokątnym stosunek sumy długości przyprostokątnych do długości przeciwprostokątnej jest równy 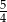 . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
Wyznacz wszystkie wartości parametru 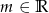 , dla których równanie
, dla których równanie
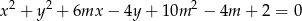
opisuje okrąg. Jaka jest największa możliwa długość tego okręgu?
W stożku o promieniu podstawy  tworząca jest nachylona do płaszczyzny podstawy pod kątem
tworząca jest nachylona do płaszczyzny podstawy pod kątem  . Przez wierzchołek stożka poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod kątem
. Przez wierzchołek stożka poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod kątem 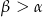 .
.
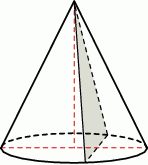
Wykaż, że pole otrzymanego przekroju stożka jest równe
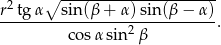
Wielomian 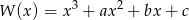 ma trzy pierwiastki rzeczywiste, które tworzą ciąg arytmetyczny o różnicy
ma trzy pierwiastki rzeczywiste, które tworzą ciąg arytmetyczny o różnicy 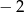 . Oblicz współczynniki
. Oblicz współczynniki 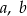 i
i  wiedząc, że
wiedząc, że 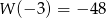 .
.
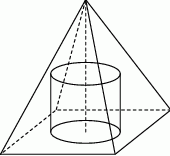
W metalowym ostrosłupie prawidłowym czworokątnym o wysokości 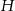 i krawędzi podstawy
i krawędzi podstawy  wydrążono otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa (patrz rysunek). Otwór wydrążono przez podstawę ostrosłupa w ten sposób, że górna podstawa walca nie wystaje poza powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób bryły?
wydrążono otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa (patrz rysunek). Otwór wydrążono przez podstawę ostrosłupa w ten sposób, że górna podstawa walca nie wystaje poza powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób bryły?