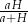/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Różne

Zadanie nr 8290211

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz długość krawędzi sześcianu, jeżeli wysokość ostrosłupa jest równa 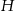H , a długość jego krawędzi podstawy jest równa a .

Rozwiązanie

Oznaczmy przez x szukaną długość krawędzi sześcianu.

PIC

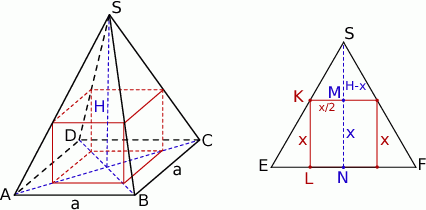
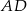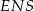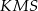Na prawym rysunku narysowaliśmy przekrój ostrosłupa płaszczyzną przechodzącą przez wysokość ostrosłupa i prostopadłą do krawędzi AD . Na tym rysunku widać kilka trójkątów podobnych, np. ENS i KMS . Z tego podobieństwa mamy

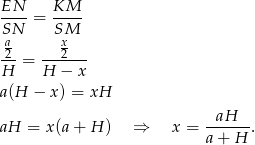
EN KM ----= ---- SaN SMx 2- = ---2--- H H − x a(H − x ) = xH aH = x(a + H ) ⇒ x = -aH---. a+ H

 
Odpowiedź: -aH- a+H

Wersja PDF