/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Różne

Zadanie nr 8442674

Dodaj do ulubionych
Dodaj do rozwiązanych

Można przyjąć, że piramida Cheopsa jest ostrosłupem prawidłowym czworokątnym o krawędzi podstawy 233 m. Długość cienia piramidy w momencie, gdy promienie słoneczne padają prostopadle do jednej ze ścian wynosi 67,5 m. Wyznacz wysokość piramidy.

Rozwiązanie

Zaczynamy od rysunku.

PIC

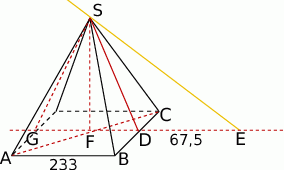
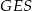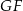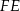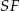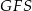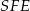Gdy się dokładnie przyjrzymy, to mamy trójkąt prostokątny GES , w którym znamy GF i FE , a mamy wyliczyć wysokość SF . Standardowy sposób to podobieństwo trójkątów GF S i SF E . Mamy z niego

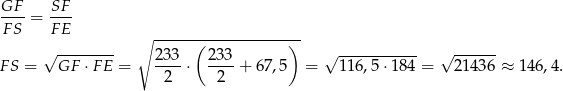
GF-- SF- F S = FE ∘ -----(------------)-- √ -------- 233- 2-33 √ ----------- √ ------ FS = GF ⋅ FE = 2 ⋅ 2 + 67,5 = 11 6,5⋅18 4 = 2143 6 ≈ 146,4.

 
Odpowiedź: Około 146,4 m

Wersja PDF