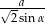/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Różne

Zadanie nr 9698504

Dodaj do ulubionych
Dodaj do rozwiązanych

Odległość środka podstawy ostrosłupa prawidłowego czworokątnego od krawędzi bocznej równa się a , a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się 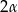2α . Oblicz wysokość ostrosłupa.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

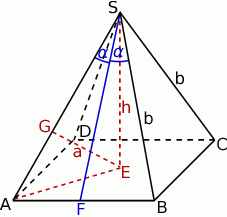
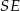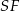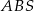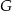Niech SE będzie wysokością ostrosłupa, SF wysokością ściany bocznej ABS , a G rzutem punktu 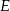E na krawędź 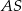AS . Oznaczmy ponadto długość krawędzi bocznej przez 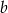b , a długość wysokości ostrosłupa przez h .

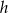Z trójkąta prostokątnego 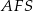AF S mamy

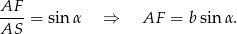
AF ----= sin α ⇒ AF = bsinα . AS

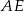Odcinek AE jest połową przekątnej kwadratu o boku 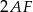2AF , czyli

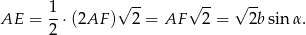
1 √ -- √ -- √ -- AE = --⋅(2AF ) 2 = AF 2 = 2b sin α. 2

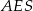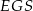Teraz wystarczy skorzystać z podobieństwa trójkątów prostokątnych AES i EGS (inny sposób to policzyć pole trójkąta 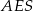AES na dwa sposoby). Mamy zatem

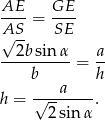
AE GE ----= ---- A√S-- SE 2b sin α a ----b-----= h- a h = √--------. 2 sin α

 
Odpowiedź: √--a--- 2sin α

Wersja PDF