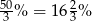/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Różne

Zadanie nr 9789077

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym czworokątnym wysokości przeciwległych ścian bocznych, poprowadzone z wierzchołka ostrosłupa, są do siebie prostopadłe.

  • Oblicz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
  • Jakim procentem objętości sześcianu, którego krawędź ma długość równą długości krawędzi podstawy danego ostrosłupa, jest objętość tego ostrosłupa?

Rozwiązanie

Zaczynamy od rysunku

PIC

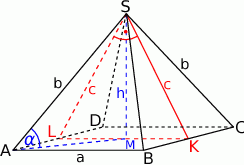
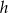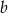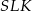  • Postaramy się obliczyć długość wysokości h i krawędzi bocznej b w zależności od długości krawędzi podstawy a . Trójkąt SLK jest prostokątny, zatem na mocy twierdzenia Pitagorasa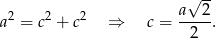
    √ -- a2 = c2 + c2 ⇒ c = a--2-. 2

    Stosujemy teraz twierdzenie Pitagorasa w trójkącie ALS

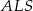
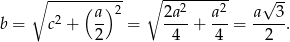
    ∘ -----(--)2- ∘ --2-----2 √ -- b = c2 + a- = 2a--+ a--= a--3-. 2 4 4 2

    Z trójkąta prostokątnego 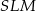SLM mamy

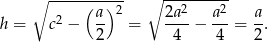
    ∘ -----(--)2- ∘ --2----2- h = c2 − a- = 2a--− a--= a. 2 4 4 2

    Teraz już łatwo obliczyć żądany sinus

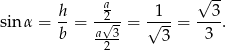
    a √ -- sinα = h-= -2√--= √1--= --3. b a--3 3 3 2

     
    Odpowiedź: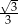 √3- 3

  • Oznaczmy przez 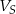VS objętość sześcianu, a przez 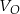VO objętość ostrosłupa. Wówczas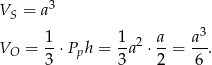
    VS = a3 3 V = 1-⋅P h = 1-a2 ⋅ a-= a-. O 3 p 3 2 6

    Liczymy szukany procent

    a3 VO- -6- 50- 2- VS ⋅10 0% = a3 ⋅100% = 3 % = 16 3% .

     
    Odpowiedź: 530% = 1623%

Wersja PDF