Zadanie nr 1010737
Podstawą ostrosłupa 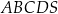 jest kwadrat
jest kwadrat 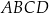 (patrz rysunek).
(patrz rysunek).
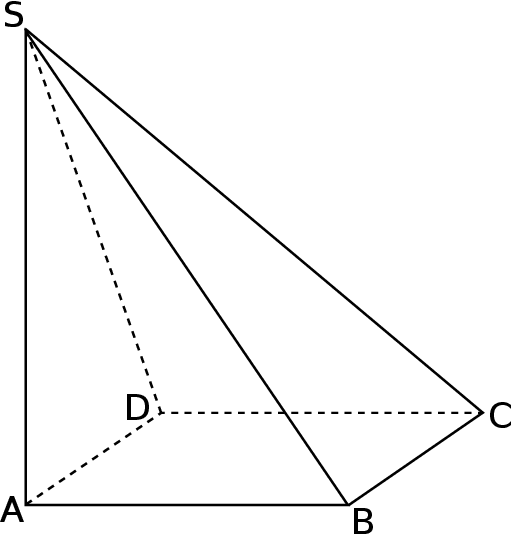
Krawędź 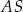 jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu 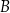 od krawędzi
od krawędzi 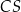 jest równa
jest równa 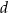 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 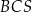 i
i 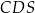 ma miarę
ma miarę 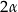 , gdzie
, gdzie 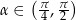 . Oblicz:
. Oblicz:
-
odległość punktu
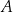 od krawędzi
od krawędzi 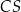
-
wysokość tego ostrosłupa.
Rozwiązanie
Dorysujmy wysokości 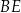 i
i 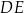 w ścianach
w ścianach 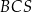 i
i 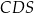 opuszczone na krawędź
opuszczone na krawędź 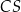 .
.
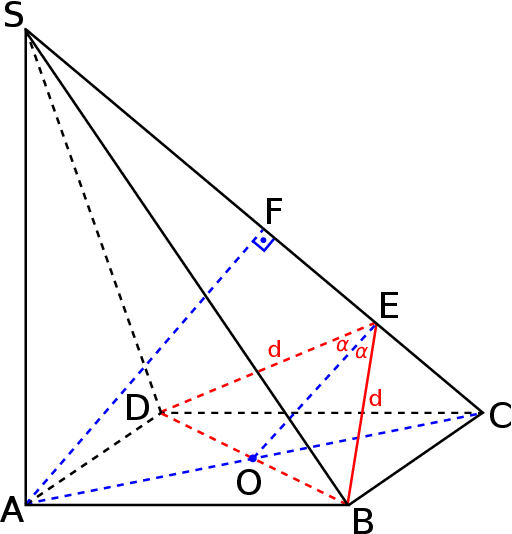
Od razu zauważmy, że krawędź 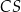 jest prostopadła do dwóch prostych w płaszczyźnie
jest prostopadła do dwóch prostych w płaszczyźnie 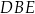 , jest więc prostopadła do całej płaszczyzny. W szczególności jeżeli
, jest więc prostopadła do całej płaszczyzny. W szczególności jeżeli 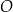 jest środkiem kwadratu w podstawie to
jest środkiem kwadratu w podstawie to 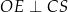 (bo
(bo 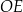 leży w płaszczyźnie
leży w płaszczyźnie 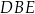 ). Ponadto, ponieważ płaszczyzna
). Ponadto, ponieważ płaszczyzna 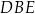 jest prostopadła do krawędzi kąta dwuściennego między ścianami
jest prostopadła do krawędzi kąta dwuściennego między ścianami 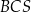 i
i 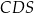 , mamy
, mamy
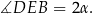
Wiemy też z treści, że
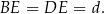
-
Poprowadźmy wysokość
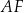 w trójkącie
w trójkącie 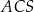 . Długość tej wysokości to dokładnie odległość punktu
. Długość tej wysokości to dokładnie odległość punktu 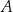 od krawędzi
od krawędzi 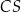 . Jak już wcześniej zauważyliśmy,
. Jak już wcześniej zauważyliśmy, 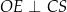 , czyli odcinki
, czyli odcinki 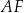 i
i 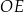 są równoległe. To oznacza, że
są równoległe. To oznacza, że 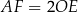 (bo
(bo 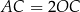 ). Długość odcinka
). Długość odcinka 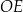 możemy wyliczyć z trójkąta prostokątnego
możemy wyliczyć z trójkąta prostokątnego 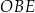 .
. 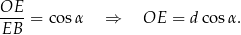
Zatem
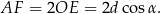
Odpowiedź: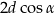
-
Zauważmy, że trójkąty
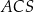 i
i 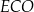 są oba prostokątne i mają wspólny kąt przy wierzchołku
są oba prostokątne i mają wspólny kąt przy wierzchołku 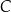 , są więc podobne. Zatem
, są więc podobne. Zatem 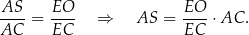
Wiemy już, że
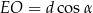 , ponadto
, ponadto 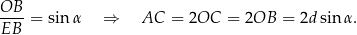
Pozostało jeszcze wyliczyć
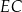 . Korzystamy z twierdzenia Pitagorasa w trójkącie
. Korzystamy z twierdzenia Pitagorasa w trójkącie 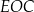 .
. 
(wyrażenie pod pierwiastkiem jest dodatnie, bo
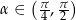 ). Mamy więc
). Mamy więc 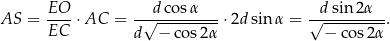
Odpowiedź: