Zadanie nr 1532036
Podstawą ostrosłupa 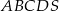 jest romb
jest romb 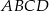 , w którym
, w którym 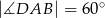 . Krawędź
. Krawędź 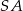 jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany
jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany 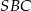 do płaszczyzny podstawy.
do płaszczyzny podstawy.
Rozwiązanie
Najtrudniejsze w tym zadaniu jest wykonanie odpowiedniego rysunku, tak aby prawidłowo zaznaczyć kąt nachylenia ściany 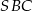 do płaszczyzny podstawy.
do płaszczyzny podstawy.
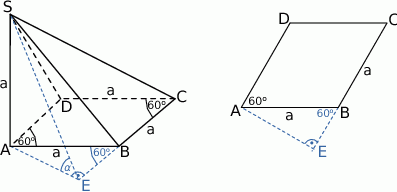
Aby móc zaznaczyć kąt nachylenia ściany 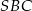 do płaszczyzny podstawy musimy narysować płaszczyznę prostopadłą do prostej
do płaszczyzny podstawy musimy narysować płaszczyznę prostopadłą do prostej 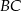 (czyli wspólnej krawędzi płaszczyzn:
(czyli wspólnej krawędzi płaszczyzn: 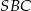 i
i 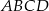 ). Taką płaszczyzną jest płaszczyzna
). Taką płaszczyzną jest płaszczyzna 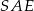 , gdzie
, gdzie 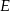 jest rzutem punktu
jest rzutem punktu 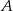 na prostą
na prostą 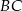 . Rzeczywiście, płaszczyzna ta zwiera dwie nierównoległe proste:
. Rzeczywiście, płaszczyzna ta zwiera dwie nierównoległe proste: 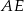 i
i 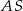 prostopadłe do
prostopadłe do 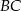 . Jest więc prostopadła do
. Jest więc prostopadła do 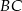 .
.
Po wykonaniu dobrego rysunku rachunki są już bardzo proste. Z trójkąta prostokątnego 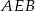 mamy
mamy
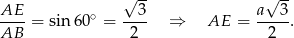
W trójkącie prostokątnym 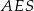 mamy
mamy
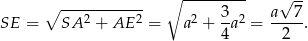
Stąd
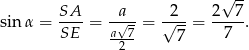
Odpowiedź: