/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny

Zadanie nr 5438267

Dodaj do ulubionych
Dodaj do rozwiązanych

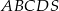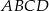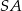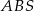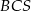Podstawą ostrosłupa ABCDS jest prostokąt ABCD , a krawędź boczna SA jest jego wysokością. Wykaż, że suma kwadratów pól ścian ABS i BCS jest równa sumie kwadratów pól ścian 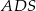ADS i DCS .

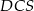Rozwiązanie

Rozpoczynamy od rysunku – oznaczmy od razu 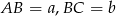AB = a,BC = b i SA = H .

PIC

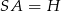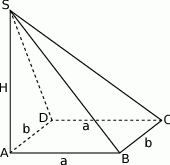
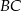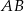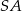Zauważmy, że krawędź BC jest prostopadła do AB i do SA , czyli jest prostopadła do ściany 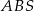ABS . Zatem jest prostopadła do każdej prostej w tej ścianie, czyli trójkąt 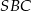SBC jest prostokątny (jeżeli ktoś woli, to może skorzystać z twierdzenia o trzech prostych prostopadłych). Podobnie zauważamy, że krawędź 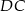DC jest prostopadła do ściany 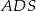ADS , czyli trójkąt 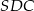SDC też jest prostokątny. Teraz łatwo policzyć interesujące nas pola.

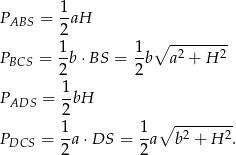
P = 1aH ABS 2 1 1 ∘ -------- PBCS = -b ⋅BS = --b a2 + H 2 2 2 PADS = 1-bH 2 1- 1-∘ -2-----2 PDCS = 2 a⋅DS = 2a b + H .

Mamy zatem

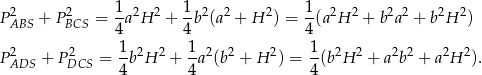
P2 + P2 = 1a2H 2 + 1b 2(a2 + H 2) = 1(a2H 2 + b2a2 + b2H 2) ABS BCS 4 4 4 2 2 1 2 2 1 2 2 2 1 2 2 2 2 2 2 PADS + PDCS = --b H + -a (b + H ) = --(b H + a b + a H ). 4 4 4

Widać zatem, że 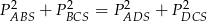2 2 2 2 PABS + PBCS = PADS + PDCS .

Wersja PDF