/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny

Zadanie nr 6080252

Dodaj do ulubionych
Dodaj do rozwiązanych

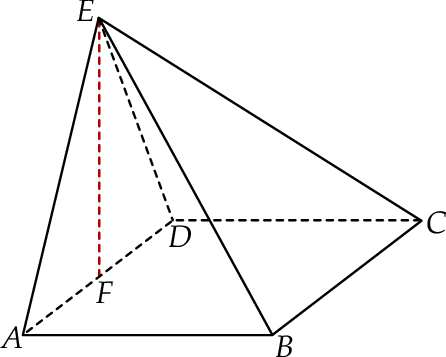
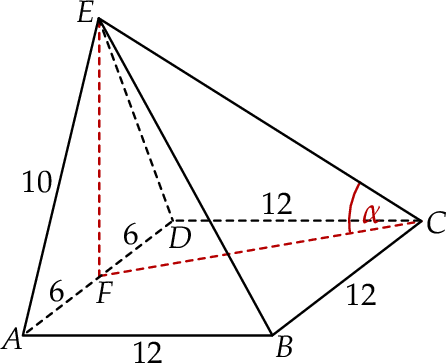
Podstawą ostrosłupa 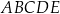ABCDE jest kwadrat o boku długości 12. Spodek 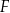F wysokości 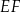EF ostrosłupa jest środkiem krawędzi 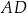AD . Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi 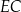EC do płaszczyzny podstawy.

ZINFO-FIGURE

Rozwiązanie

Dorysujmy odcinek 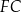FC .

ZINFO-FIGURE

Trójkąt 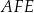AF E jest prostokątny, więc korzystając z twierdzenia Pitagorasa mamy

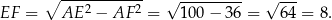
∘ ------------ √ --------- √ --- EF = AE 2 − AF 2 = 100 − 36 = 64 = 8.

Również z twierdzenia Pitagorasa obliczamy długość odcinka 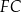F C .

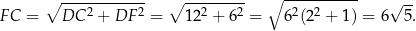
∘ ---2------2- ∘ --2----2- ∘ --2--2----- √ -- F C = DC + DF = 12 + 6 = 6 (2 + 1 ) = 6 5.

Kąt nachylenia krawędzi 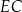EC do płaszczyzny podstawy to kąt 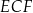ECF . Tangens tego kąta jest równy

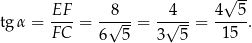
√ -- EF-- --8-- --4-- 4--5- tg α = FC = 6√ 5-= 3√ 5-= 15 .

 
Odpowiedź: 4√-5 15

Wersja PDF