Zadanie nr 6566476
Podstawą ostrosłupa jest romb, którego pole wynosi 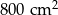 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 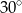 . Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
. Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
- promień tego okręgu,
- pole powierzchni bocznej ostrosłupa.
Rozwiązanie
Rozpoczynamy od rysunku.
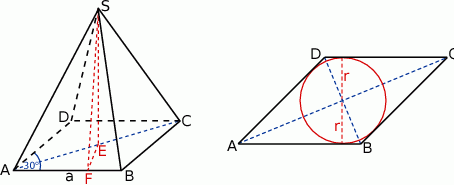
Zauważmy, że podanego pola i kąta ostrego rombu łatwo obliczyć długość jego boku (korzystając ze wzoru na pole z sinusem).

Promień okręgu wpisanego w romb to połowa jego wysokości, a wysokość łatwo obliczyć, gdy znamy pole i bok rombu.
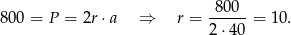
Jeżeli 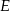 jest środkiem okręgu wpisanego w romb w podstawie, a
jest środkiem okręgu wpisanego w romb w podstawie, a 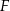 jest rzutem punktu
jest rzutem punktu 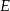 na krawędź
na krawędź 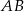 , to płaszczyzna
, to płaszczyzna 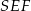 jest prostopadła do krawędzi
jest prostopadła do krawędzi 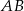 (bo zawiera dwie proste:
(bo zawiera dwie proste: 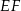 i
i 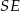 prostopadłe do
prostopadłe do 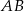 ). w takim razie
). w takim razie 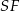 jest wysokością ściany bocznej. Z trójkąta prostokątnego
jest wysokością ściany bocznej. Z trójkąta prostokątnego 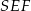 mamy
mamy
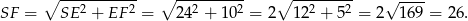
Ponieważ spodek wysokości jest środkiem okręgu wpisanego w podstawę, dokładnie w ten sam sposób możemy obliczyć wysokości pozostałych ścian bocznych, więc wszystkie te wysokości będą miały tę samą długość. Pole powierzchni bocznej ostrosłupa jest więc równe
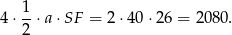
Odpowiedź: Promień: 10 cm, pole boczne: