/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny

Zadanie nr 7828478

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa 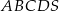ABCDS jest równoległobok 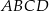ABCD o przekątnej długości 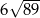√ --- 6 89 i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku 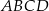ABCD , a jego ściany boczne są trójkątami ostrokątnymi. 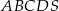Oblicz długość krótszej z krawędzi bocznych ostrosłupa ABCDS .

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.