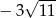Zadanie nr 9049853
Podstawą ostrosłupa 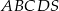 jest prostokąt
jest prostokąt 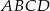 . Spodkiem wysokości ostrosłupa jest środek
. Spodkiem wysokości ostrosłupa jest środek 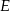 krawędzi
krawędzi 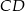 . Oblicz tangens kąta między ścianami bocznymi
. Oblicz tangens kąta między ścianami bocznymi 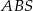 i
i 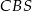 tego ostrosłupa jeżeli
tego ostrosłupa jeżeli 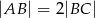 i
i 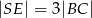 .
.
Rozwiązanie
Niech 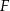 będzie środkiem krawędzi
będzie środkiem krawędzi 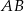 oraz
oraz 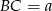 . Wtedy z założenia
. Wtedy z założenia 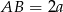 i
i 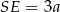 .
.
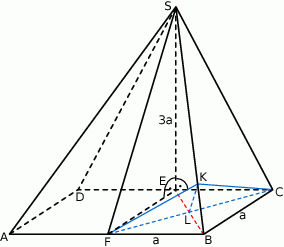
Zauważmy, że podstawą ostrosłupa 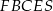 jest kwadrat
jest kwadrat 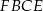 , a wysokością tego ostrosłupa jest jego krawędź
, a wysokością tego ostrosłupa jest jego krawędź 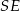 . W szczególności ściany
. W szczególności ściany 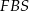 i
i 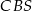 są przystające i kąt między tymi ścianami to kąt między wysokościami
są przystające i kąt między tymi ścianami to kąt między wysokościami 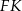 i
i 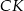 trójkątów
trójkątów 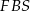 i
i 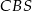 (płaszczyzna
(płaszczyzna 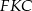 jest prostopadła do krawędzi wspólnej
jest prostopadła do krawędzi wspólnej 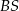 ścian
ścian 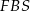 i
i 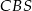 , więc kąt
, więc kąt 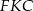 jest interesującym nas kątem między tymi ścianami).
jest interesującym nas kątem między tymi ścianami).
Obliczamy na początek długości odcinków 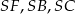 .
.
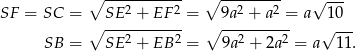
Zauważmy teraz, że trójkąty 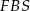 i
i 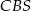 są prostokątne – wynika to z tego, że krawędzie
są prostokątne – wynika to z tego, że krawędzie 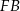 i
i 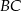 są prostopadłe odpowiednio do ścian
są prostopadłe odpowiednio do ścian 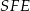 i
i 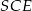 . Wysokość
. Wysokość 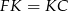 trójkąta prostokątnego
trójkąta prostokątnego 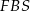 możemy obliczyć porównując dwa wzory na pole.
możemy obliczyć porównując dwa wzory na pole.
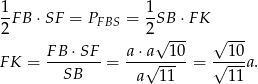
Tangens kąta 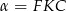 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Odcinek 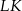 jest wysokością w trójkącie równoramiennym
jest wysokością w trójkącie równoramiennym 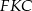 , więc
, więc
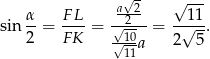
Obliczamy teraz 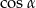 .
.
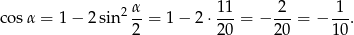
Obliczamy teraz 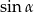 .
.
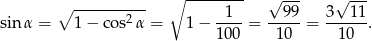
Interesujący nas tangens jest więc równy
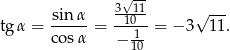
Sposób II
Tym razem obliczamy 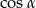 pisząc twierdzenie cosinusów w trójkącie
pisząc twierdzenie cosinusów w trójkącie  .
.
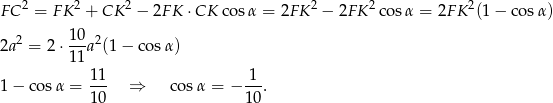
Liczymy teraz 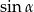 .
.
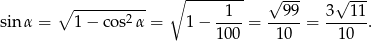
Interesujący nas tangens jest więc równy
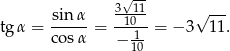
Odpowiedź: