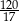Zadanie nr 9114073
Podstawą ostrosłupa 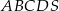 jest trapez równoramienny
jest trapez równoramienny 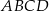 , którego ramiona mają długość
, którego ramiona mają długość 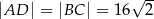 i tworzą z podstawą
i tworzą z podstawą 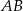 kąt ostry o mierze
kąt ostry o mierze 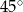 . Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem
. Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem  takim, że
takim, że 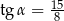 . Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej 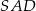 .
.
Rozwiązanie
Rozpoczynamy od naszkicowania opisanej sytuacji.
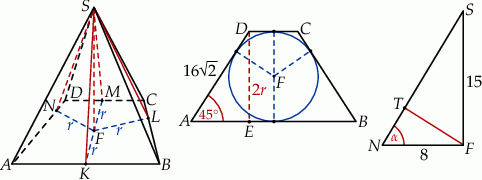
Aby zaznaczyć kąty nachylenia ścian bocznych do płaszczyzny podstawy zaznaczyliśmy na rysunku rzuty 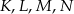 spodka wysokości
spodka wysokości 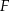 na boki trapezu
na boki trapezu  . Krawędź
. Krawędź 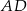 jest prostopadła do
jest prostopadła do 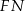 i do
i do 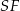 , więc jest prostopadła do płaszczyzny
, więc jest prostopadła do płaszczyzny 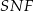 – to oznacza, że kąt
– to oznacza, że kąt 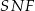 jest kątem między ścianą boczną
jest kątem między ścianą boczną 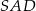 , a płaszczyzną podstawy. Dokładnie tak samo jest w przypadku pozostałych ścian bocznych.
, a płaszczyzną podstawy. Dokładnie tak samo jest w przypadku pozostałych ścian bocznych.
Zauważmy teraz, że trójkąty 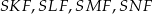 są prostokątne i mają z założenia takie same kąty ostre. Mają ponadto wspólną przyprostokątną
są prostokątne i mają z założenia takie same kąty ostre. Mają ponadto wspólną przyprostokątną 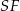 . To oznacza, że są one przystające, czyli w szczególności
. To oznacza, że są one przystające, czyli w szczególności 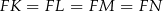 , czyli punkt
, czyli punkt 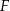 jest środkiem okręgu wpisanego w podstawę
jest środkiem okręgu wpisanego w podstawę 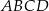 (bo jego odległość od każdego z boków tego czworokąta jest taka sama).
(bo jego odległość od każdego z boków tego czworokąta jest taka sama).
Długość promienia okręgu wpisanego w podstawę obliczamy z trójkąta 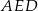 .
.
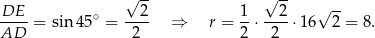
Patrzymy teraz na trójkąt prostokątny  .
.
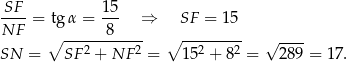
Ponieważ płaszczyzna  jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 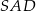 odległość punktu
odległość punktu 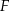 od ściany
od ściany 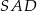 to długość wysokości
to długość wysokości 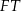 trójkąta
trójkąta 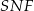 opuszczonej na przeciwprostokątną
opuszczonej na przeciwprostokątną 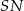 . Możemy ją obliczyć z podobieństwa trójkątów
. Możemy ją obliczyć z podobieństwa trójkątów 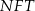 i
i 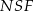 lub porównując dwa wzory na pole trójkąta
lub porównując dwa wzory na pole trójkąta  . My zrobimy to tym drugim sposobem.
. My zrobimy to tym drugim sposobem.
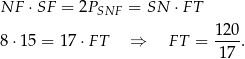
Odpowiedź: