Zadanie nr 9477617
Podstawą ostrosłupa jest kwadrat 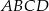 o boku długości 40. Pola ścian bocznych
o boku długości 40. Pola ścian bocznych 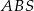 ,
, 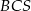 ,
, 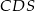 i
i 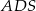 są odpowiednio równe: 740,
są odpowiednio równe: 740, 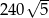 , 260 i 400. Oblicz objętość tego ostrosłupa.
, 260 i 400. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Szkicujemy ostrosłup – na rysunku zaznaczyliśmy wysokości ścian bocznych: 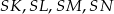 oraz wysokość ostrosłupa
oraz wysokość ostrosłupa 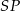 .
.
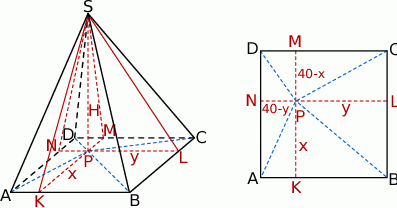
Podane pola ścian bocznych pozwalają nam obliczyć długości wysokości ścian bocznych.
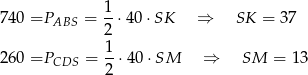
Jeżeli 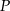 jest spodkiem wysokości ostrosłupa i oznaczymy
jest spodkiem wysokości ostrosłupa i oznaczymy 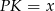 to
to 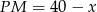 . Wartość
. Wartość  możemy wyznaczyć pisząc twierdzenia Pitagorasa w trójkątach
możemy wyznaczyć pisząc twierdzenia Pitagorasa w trójkątach 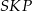 i
i 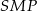 .
.
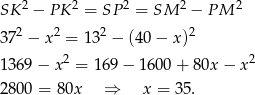
Raz jeszcze stosujemy twierdzenie Pitagorasa, aby obliczyć wysokość ostrosłupa.
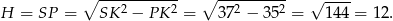
Objętość ostrosłupa jest więc równa
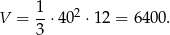
Zauważmy, że informacja o polach ścian 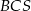 i
i 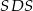 okazała się zbędna.
okazała się zbędna.
Odpowiedź: 6400

