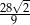Zadanie nr 9646997
Podstawą ostrosłupa 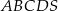 jest trapez
jest trapez 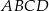 . Przekątna
. Przekątna 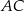 tego trapezu ma długość
tego trapezu ma długość 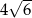 , jest prostopadła do ramienia
, jest prostopadła do ramienia 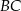 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 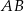 tego trapezu kąt o mierze
tego trapezu kąt o mierze 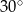 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 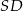 .
.
Rozwiązanie
Rozpoczynamy od naszkicowania opisanej sytuacji – aby to zrobić zauważmy, że z treści wynika, że podstawami trapezu są odcinki 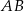 i
i 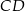 oraz
oraz 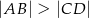 .
.
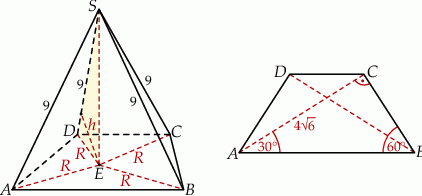
Zauważmy jeszcze, że z informacji o tym, że wszystkie krawędzie boczne mają tę samą długość wynika, że trójkąty prostokątne 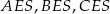 i
i  są przystające, więc
są przystające, więc 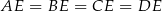 , co z kolei oznacza, że spodek
, co z kolei oznacza, że spodek 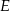 wysokości ostrosłupa jest środkiem okręgu opisanego na trapezie
wysokości ostrosłupa jest środkiem okręgu opisanego na trapezie 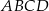 (w szczególności trapez ten musi być równoramienny).
(w szczególności trapez ten musi być równoramienny).
Skupmy się teraz na obliczeniu promienia 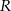 okręgu opisanego na trapezie
okręgu opisanego na trapezie 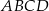 . Można to zrobić korzystając z twierdzenia sinusów w trójkącie
. Można to zrobić korzystając z twierdzenia sinusów w trójkącie 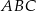 , ale można też zrobić to prościej – wystarczy zauważyć, że średnicą okręgu opisanego na trójkącie prostokątnym
, ale można też zrobić to prościej – wystarczy zauważyć, że średnicą okręgu opisanego na trójkącie prostokątnym 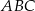 jest przeciwprostokątna
jest przeciwprostokątna 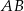 (nie będzie to nam potrzebne, ale to oznacza, że punkt
(nie będzie to nam potrzebne, ale to oznacza, że punkt 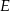 jest tak naprawdę środkiem krawędzi
jest tak naprawdę środkiem krawędzi 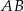 ). Mamy zatem
). Mamy zatem
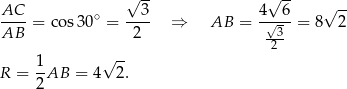
Patrzymy teraz na trójkąt prostokątny 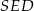 . Obliczamy najpierw długość jego przyprostokątnej
. Obliczamy najpierw długość jego przyprostokątnej 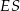 .
.
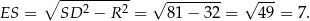
Teraz obliczamy wysokość 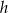 tego trójkąta opuszczoną na przeciwprostokątną – porównujemy dwa wzory na pole trójkąta
tego trójkąta opuszczoną na przeciwprostokątną – porównujemy dwa wzory na pole trójkąta 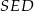 .
.
Odpowiedź: