Zadanie nr 9921746
Podstawą ostrosłupa 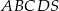 jest czworokąt
jest czworokąt 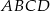 . Przekątna
. Przekątna 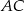 tego czworokąta ma długość
tego czworokąta ma długość 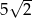 , a kąt
, a kąt 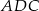 ma miarę
ma miarę 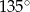 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych 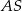 ,
, 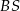 ,
, 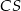 i
i 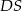 .
.
Rozwiązanie
Rozpoczynamy od naszkicowania opisanej sytuacji.
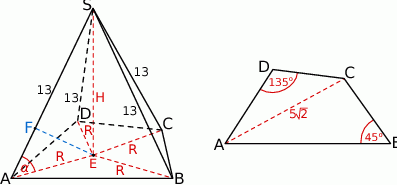
Zauważmy jeszcze, że z informacji o tym, że wszystkie krawędzie boczne mają tę samą długość wynika, że trójkąty prostokątne 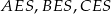 i
i 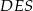 są przystające, więc
są przystające, więc 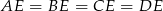 , co z kolei oznacza, że spodek
, co z kolei oznacza, że spodek 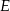 wysokości ostrosłupa jest środkiem okręgu opisanego na czworokącie
wysokości ostrosłupa jest środkiem okręgu opisanego na czworokącie 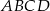 .
.
Skupmy się teraz na obliczeniu promienia 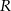 okręgu opisanego na czworokącie
okręgu opisanego na czworokącie 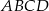 . Zrobimy to korzystając z twierdzenia sinusów w trójkącie
. Zrobimy to korzystając z twierdzenia sinusów w trójkącie 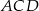 (bo okrąg opisany na czworokącie
(bo okrąg opisany na czworokącie 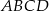 jest też okręgiem opisanym na trójkącie
jest też okręgiem opisanym na trójkącie 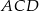 ).
).
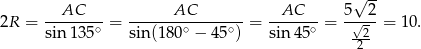
Zatem 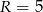 . To pozwala obliczyć wysokość
. To pozwala obliczyć wysokość 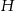 ostrosłupa
ostrosłupa
Niech 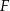 będzie rzutem spodka wysokości
będzie rzutem spodka wysokości 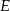 na krawędź
na krawędź 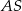 . Jak już zauważyliśmy wcześniej, trójkąty
. Jak już zauważyliśmy wcześniej, trójkąty 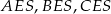 i
i 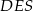 są przystające, więc interesująca nas suma odległości punktu
są przystające, więc interesująca nas suma odległości punktu 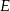 od krawędzi bocznych jest równa
od krawędzi bocznych jest równa 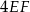 . Długość odcinka
. Długość odcinka 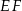 obliczamy porównując dwa wzory na pole trójkąta prostokątnego
obliczamy porównując dwa wzory na pole trójkąta prostokątnego 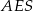 .
.
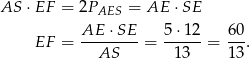
Zatem 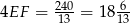 .
.
Odpowiedź: