Zadanie nr 1757770
W trójkącie 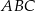 odcinek
odcinek 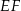 o końcach należących do boków odpowiednio
o końcach należących do boków odpowiednio 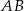 i
i 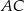 przecina środkową
przecina środkową 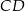 w punkcie
w punkcie 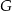 , oraz odcinek
, oraz odcinek 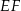 jest równoległy do odcinka
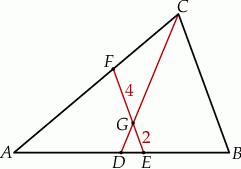
jest równoległy do odcinka 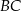 (patrz rysunek). Oblicz długość odcinka
(patrz rysunek). Oblicz długość odcinka 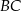 wiedząc, że
wiedząc, że 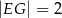 i
i 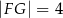 .
.
Rozwiązanie
Oznaczmy 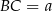 .
.
Sposób I
Dwa razy korzystamy z twierdzenia Talesa (podobieństwa trójkątów).
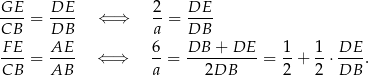
Podstawiamy teraz 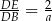 z pierwszej równości do drugiej
z pierwszej równości do drugiej
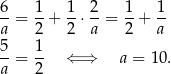
Sposób II
Niech 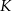 będzie punktem symetrycznym do
będzie punktem symetrycznym do 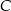 względem punktu
względem punktu 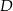 . Otrzymujemy w ten sposób równoległobok o przekątnych
. Otrzymujemy w ten sposób równoległobok o przekątnych 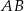 ,
, 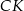 i środku
i środku 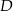 .
.
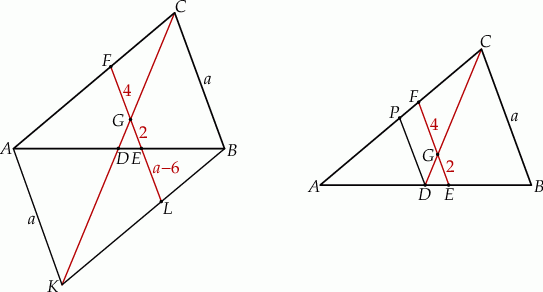
Jeżeli 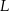 jest punktem przecięcia prostej
jest punktem przecięcia prostej 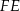 z odcinkiem
z odcinkiem 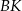 , to
, to
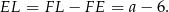
Korzystamy teraz z podobieństw trójkątów 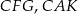 oraz
oraz 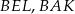
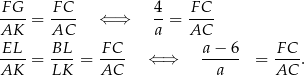
Mamy stąd
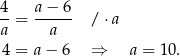
Sposób III
Tym razem dorysujmy środek 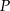 odcinka
odcinka 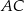 . Wtedy
. Wtedy 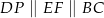 i
i 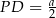 . Trójkąty
. Trójkąty 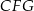 i
i 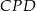 są podobne, więc
są podobne, więc
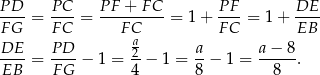
Podobnie, z podobieństwa trójkątów 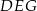 i
i 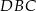 mamy
mamy
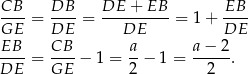
Mamy zatem
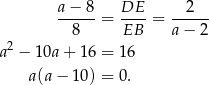
Zatem 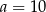 .
.
Odpowiedź: 10

