Zadanie nr 1869408
Okrąg o promieniu 4 jest wpisany w trójkąt. Punkt styczności podzielił jeden z boków na odcinki o długości 6 i 8. Oblicz długości boków tego trójkąta.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
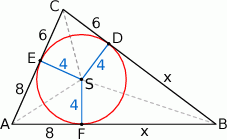
Jeżeli 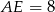 i
i 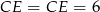 , to
, to 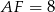 i
i 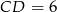 (odcinki stycznych do okręgu wpisanego w trójkąt). Możemy ponadto oznaczyć
(odcinki stycznych do okręgu wpisanego w trójkąt). Możemy ponadto oznaczyć 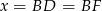 .
.
Sposób I
Aby obliczyć  , porównamy dwa wzory na pole trójkąta. Jeden z tych wzorów to wzór Herona
, porównamy dwa wzory na pole trójkąta. Jeden z tych wzorów to wzór Herona
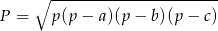
na pole trójkąta o bokach długości 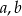 i
i  , gdzie
, gdzie 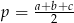 jest połową obwodu trójkąta.
jest połową obwodu trójkąta.
Drugi wzór to
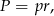
gdzie  jest promieniem okręgu wpisanego w trójkąt.
jest promieniem okręgu wpisanego w trójkąt.
W naszej sytuacji mamy 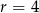 i
i
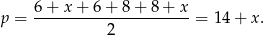
Stąd
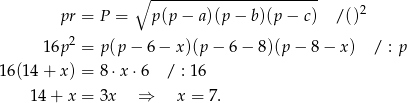
Boki trójkąta 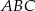 mają więc długości
mają więc długości
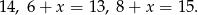
Sposób II
Tym razem skorzystamy z twierdzenia sinusów. Zauważmy najpierw, że
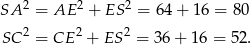
Jeżeli teraz oznaczymy 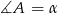 i
i 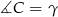 , to
, to
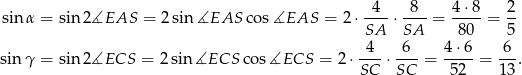
Korzystamy teraz z twierdzenia sinusów.
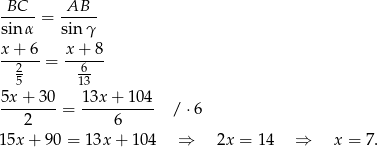
Boki trójkąta 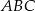 mają więc długości
mają więc długości
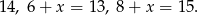
Odpowiedź: 13, 14, 15

