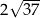/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Długości boków

Zadanie nr 2033244

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie kąt między bokami o długościach 8 i 6 jest równy 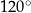∘ 120 . Jaką długość ma trzeci bok trójkąta?

Rozwiązanie

Zacznijmy od schematycznego rysunku.

ZINFO-FIGURE

Długość trzeciego boku obliczymy korzystając z twierdzenia cosinusów.

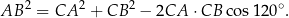
AB 2 = CA 2 + CB 2 − 2CA ⋅CB cos 120∘.

Aby to zrobić zauważmy najpierw, że

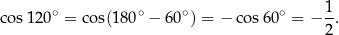
∘ ∘ ∘ ∘ 1- cos12 0 = cos(180 − 60 ) = − cos 60 = − 2 .

Mamy zatem

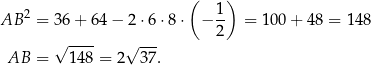
( 1 ) AB 2 = 36 + 64 − 2 ⋅6⋅ 8⋅ − -- = 1 00+ 48 = 148 √ ---- √ --- 2 AB = 148 = 2 37.

 
Odpowiedź: √ --- 2 37

Wersja PDF