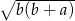Zadanie nr 2808426
Dane są długości boków  i
i 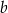 trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku
trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku 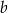 .
.
Rozwiązanie
Sposób I
Dorysujmy dwusieczną 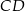 i niech
i niech 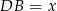 .
.
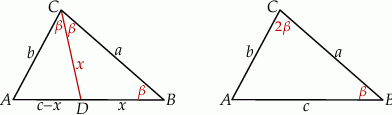
Trójkąt 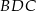 jest równoramienny, więc
jest równoramienny, więc 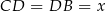 . Ponadto
. Ponadto
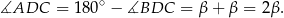
To oznacza, że trójkąty 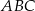 i
i 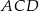 mają równe kąty, więc są podobne. Z tego podobieństwa mamy
mają równe kąty, więc są podobne. Z tego podobieństwa mamy
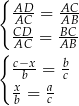
Z drugiej równości mamy 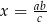 i wtedy z pierwszej równości mamy
i wtedy z pierwszej równości mamy
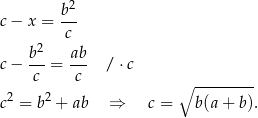
Sposób II
Spróbujemy trzeci bok obliczyć z twierdzenia cosinusów, najpierw jednak wyliczymy 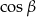 . Z twierdzenia sinusów mamy
. Z twierdzenia sinusów mamy
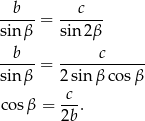
Piszemy teraz twierdzenie cosinusów
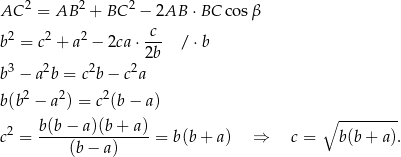
Odpowiedź: