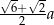/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Długości boków

Zadanie nr 4536814

Dodaj do ulubionych
Dodaj do rozwiązanych

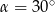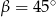W trójkącie ABC dane są kąty ∘ α = 30 , ∘ β = 45 oraz długość a boku leżącego naprzeciw kąta α . Oblicz długości pozostałych boków.

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

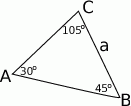
Oczywiście trzeci kąt trójkąta ma miarę 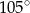105 ∘ . W szczególności

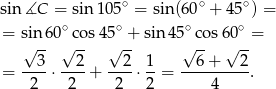
∘ ∘ ∘ sin ∡C = sin1 05 = sin(60 + 45 ) = = sin6 0∘cos 45∘ + sin 45∘ cos 60∘ = √ -- √ -- √ -- √ -- √ -- = --3-⋅ --2+ --2-⋅ 1-= --6-+---2. 2 2 2 2 4

Na mocy twierdzenia sinusów mamy

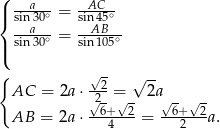
( |{ sina30∘-= siAnC45∘ --a-∘-= --AB--∘ |( sin30 sin105 { √-2 √ -- AC = 2a ⋅√2-=√- 2a√- √- AB = 2a ⋅--6+--2-= -6+--2a. 4 2

 
Odpowiedź: 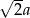√ -- 2a , √6+-√2- 2 a

Wersja PDF