Zadanie nr 4730671
W trójkącie 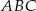 dane są:
dane są: 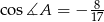 ,
, 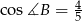 i
i 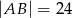 . Oblicz długości pozostałych boków trójkąta
. Oblicz długości pozostałych boków trójkąta 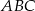 .
.
Rozwiązanie
Szkicujemy trójkąt.
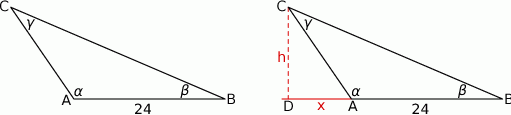
Obliczamy z podanych cosinusów sinusy kątów 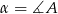 i
i 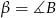 .
.
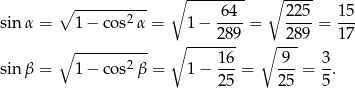
Sposób I
Obliczamy 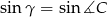 .
.
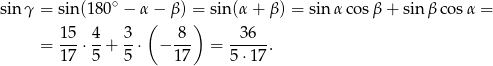
Korzystamy teraz z twierdzenia sinusów.
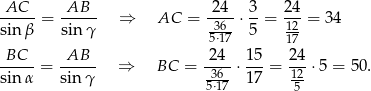
Sposób II
Niech 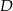 będzie spodkiem wysokości opuszczonej z wierzchołka
będzie spodkiem wysokości opuszczonej z wierzchołka 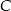 na bok
na bok 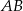 i niech
i niech 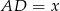 . Z trójkątów prostokątnych
. Z trójkątów prostokątnych 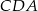 i
i 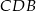 mamy
mamy
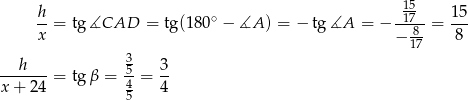
Podstawiamy teraz 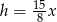 z pierwszej równości do drugiej i mamy
z pierwszej równości do drugiej i mamy
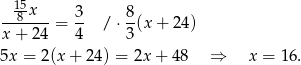
Stąd 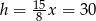 i
i
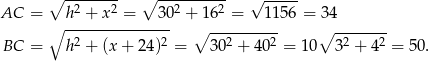
Odpowiedź: 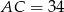 ,
,