Zadanie nr 6930679
Promień okręgu wpisanego w trójkąt o bokach 5 i 8 jest równy równy 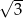 , a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
, a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
Rozwiązanie
Szkicujemy trójkąt – oznaczmy przez 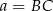 jego trzeci bok i niech
jego trzeci bok i niech 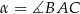 .
.
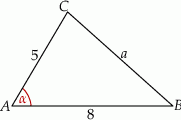
Musimy jakość wykorzystać podaną informację o promieniu okręgu wpisanego. Jest w zasadzie tylko jeden sposób, żeby to zrobić – wzór na pole trójkąta: 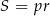 , gdzie
, gdzie 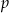 jest połową jego obwodu.
jest połową jego obwodu.
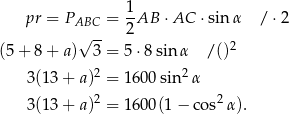
Powód, dla którego przekształcaliśmy powyższą równość tak, aby powiązać ze sobą  i
i 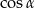 jest bardzo prosty – chcemy w tym miejscu skorzystać z twierdzenia cosinusów:
jest bardzo prosty – chcemy w tym miejscu skorzystać z twierdzenia cosinusów:
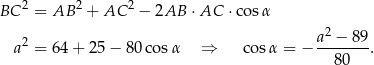
Sposób I
Podstawiamy obliczony 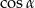 do wcześniej otrzymanej równości.
do wcześniej otrzymanej równości.
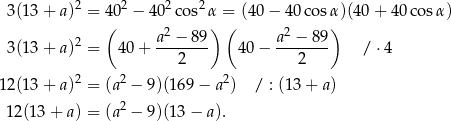
Teraz mamy dwie możliwości. Ponieważ  ma być liczbą całkowitą, oraz
ma być liczbą całkowitą, oraz 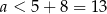 , możemy sprawdzić, która z 12 możliwych wartości
, możemy sprawdzić, która z 12 możliwych wartości  spełnia powyższe równanie – gdy to zrobimy okaże się, tak jest tylko dla
spełnia powyższe równanie – gdy to zrobimy okaże się, tak jest tylko dla 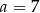 .
.
Możemy też postąpić bardziej konwencjonalnie i próbować rozwiązać otrzymane równanie wielomianowe stopnia 3.
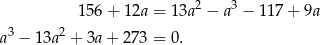
Szukamy teraz pierwiastków całkowitych – sprawdzamy dzielniki wyrazu wolnego 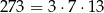 . Dodatkowo, interesują nas tylko liczby mniejsze od
. Dodatkowo, interesują nas tylko liczby mniejsze od 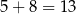 . Do sprawdzenia mamy więc
. Do sprawdzenia mamy więc 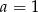 ,
, 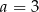 i
i 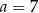 . Gdy to zrobimy, okaże się, że spośród tych liczb tylko
. Gdy to zrobimy, okaże się, że spośród tych liczb tylko 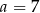 spełnia powyższe równanie.
spełnia powyższe równanie.
Sposób II
Tak jak poprzednio podstawiamy 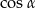 do otrzymanej wcześniej równości.
do otrzymanej wcześniej równości.
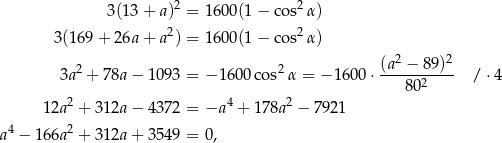
Szukamy teraz pierwiastków całkowitych – sprawdzamy dzielniki wyrazu wolnego 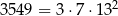 . Dodatkowo, interesują nas tylko liczby mniejsze od
. Dodatkowo, interesują nas tylko liczby mniejsze od 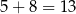 . Do sprawdzenia mamy więc
. Do sprawdzenia mamy więc 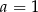 ,
, 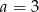 i
i 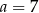 . Gdy to zrobimy, okaże się, że spośród tych liczb tylko
. Gdy to zrobimy, okaże się, że spośród tych liczb tylko 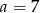 spełnia powyższe równanie.
spełnia powyższe równanie.
Sposób III
Tym razem obejdziemy się bez trygonometrii – zamiast tego użyjemy wzoru Herona.
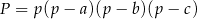
na pole trójkąta o bokach 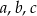 i połowie obwodu
i połowie obwodu 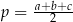 .
.
W naszej sytuacji mamy 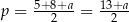 oraz
oraz
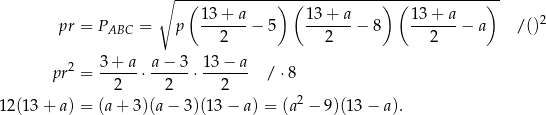
Jest to samo równanie, które otrzymaliśmy w Sposobie I – rozwiązujemy je dokładnie w ten sam sposób.
Odpowiedź: 7

