/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Długości boków

Zadanie nr 7733496

Wysokość trójkąta 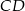CD ma długość 4 i dzieli bok 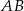AB na odcinki, z których krótszy 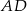AD ma długość 2, a kąt 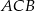ACB na kąty, których stosunek miar jest równy 1:2. Oblicz długość boku 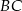BC tego trójkąta.

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

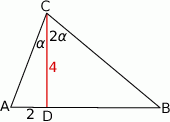
Zauważmy, że w trójkącie prostokątnym 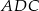ADC możemy łatwo obliczyć funkcje trygonometryczne kąta α .

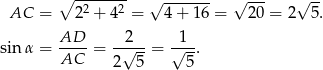
∘ ------- √ ------- √ --- √ -- AC = 22 + 42 = 4 + 16 = 20 = 2 5. sinα = AD--= -√2--= √1--. AC 2 5 5

To pozwala nam obliczyć 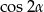c os2α .

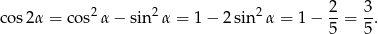
cos 2α = co s2α − sin2α = 1− 2sin2α = 1− 2-= 3. 5 5

Patrzymy teraz na trójkąt 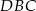DBC .

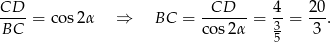
CD CD 4 20 ---- = co s2α ⇒ BC = -------= --= --. BC cos 2α 35 3

 
Odpowiedź: BC = 20- 3

Wersja PDF