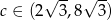Zadanie nr 7792830
Dane są dwa boki trójkąta: 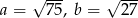 . Jaką długość może przyjmować trzeci bok trójkąta?
. Jaką długość może przyjmować trzeci bok trójkąta?
Rozwiązanie
Trójkąt o bokach 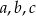 istnieje o ile
istnieje o ile
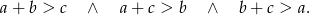
Tak naprawdę, to wystarczy aby była spełniona tylko jedna z tych nierówności: ta w której najdłuższy bok jest po prawej stronie.
Zauważmy najpierw, że 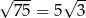 i
i 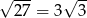 . Jeżeli
. Jeżeli  jest długością trzeciego boku trójkąta, to muszą być spełnione nierówności
jest długością trzeciego boku trójkąta, to muszą być spełnione nierówności
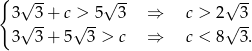
(nierówności są dwie, a nie trzy, bo 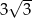 na pewno nie jest najdłuższym bokiem). Mamy zatem
na pewno nie jest najdłuższym bokiem). Mamy zatem 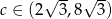 .
.
Odpowiedź: