/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność

Zadanie nr 1662349

Dodaj do ulubionych
Dodaj do rozwiązanych

Do dwóch stycznych zewnętrznie okręgów poprowadzono dwie wspólne styczne: jedną zewnętrzną i jedną wewnętrzną. Proste te przecinają się pod kątem 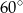60∘ . Wyznacz stosunek długości promieni tych okręgów.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

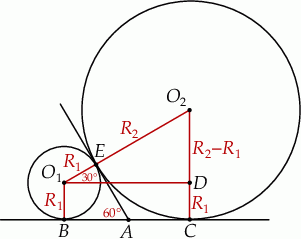
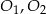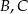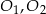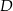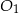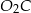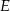Niech O 1,O 2 będą środkami okręgów, B,C rzutami punktów O 1,O 2 na wspólną styczną zewnętrzną, D rzutem punktu O 1 na prostą O2C i E punktem wspólnym okręgów. Czworokąt 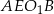AEO B 1 ma dwa kąty proste:

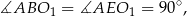
∘ ∡ABO 1 = ∡AEO 1 = 90 ,

więc

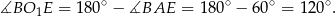
∘ ∘ ∘ ∘ ∡BO 1E = 1 80 − ∡BAE = 18 0 − 60 = 120 .

Stąd

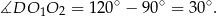
∘ ∘ ∘ ∡DO 1O 2 = 12 0 − 9 0 = 30 .

Patrzymy teraz na trójkąt prostokątny 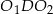O 1DO 2 .

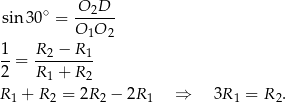
O D sin 30∘ = --2--- O1O 2 1- R-2 −-R1 2 = R 1 + R2 R 1 + R2 = 2R 2 − 2R 1 ⇒ 3R1 = R2.

 
Odpowiedź: 3:1

Wersja PDF