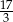Zadanie nr 3418127
Różnica promieni dwóch okręgów współśrodkowych jest równa 3. W okręgu o większym promieniu poprowadzono cięciwę styczną do drugiego okręgu. Cięciwa ta ma długość 10. Oblicz długość promieni tych okręgów.
Rozwiązanie
Zaczynamy od rysunku.
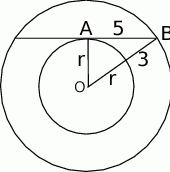
Jeżeli oznaczymy promień mniejszego okręgu przez 
, to większy okrąg ma promień 
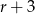. Piszemy teraz twierdzenie Pitagorasa w trójkącie 
.
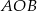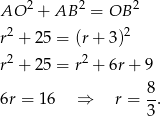
Odpowiedź: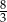 
i 
